The Experience of Maxing Out One’s Cognitive Horsepower

by Justin Skycak (@justinskycak) on

And why maximizing learning efficiency is such a big lever in maximizing student potential.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

There’s some interesting discussion about the experience of maxing out one’s cognitive horsepower in this thread:

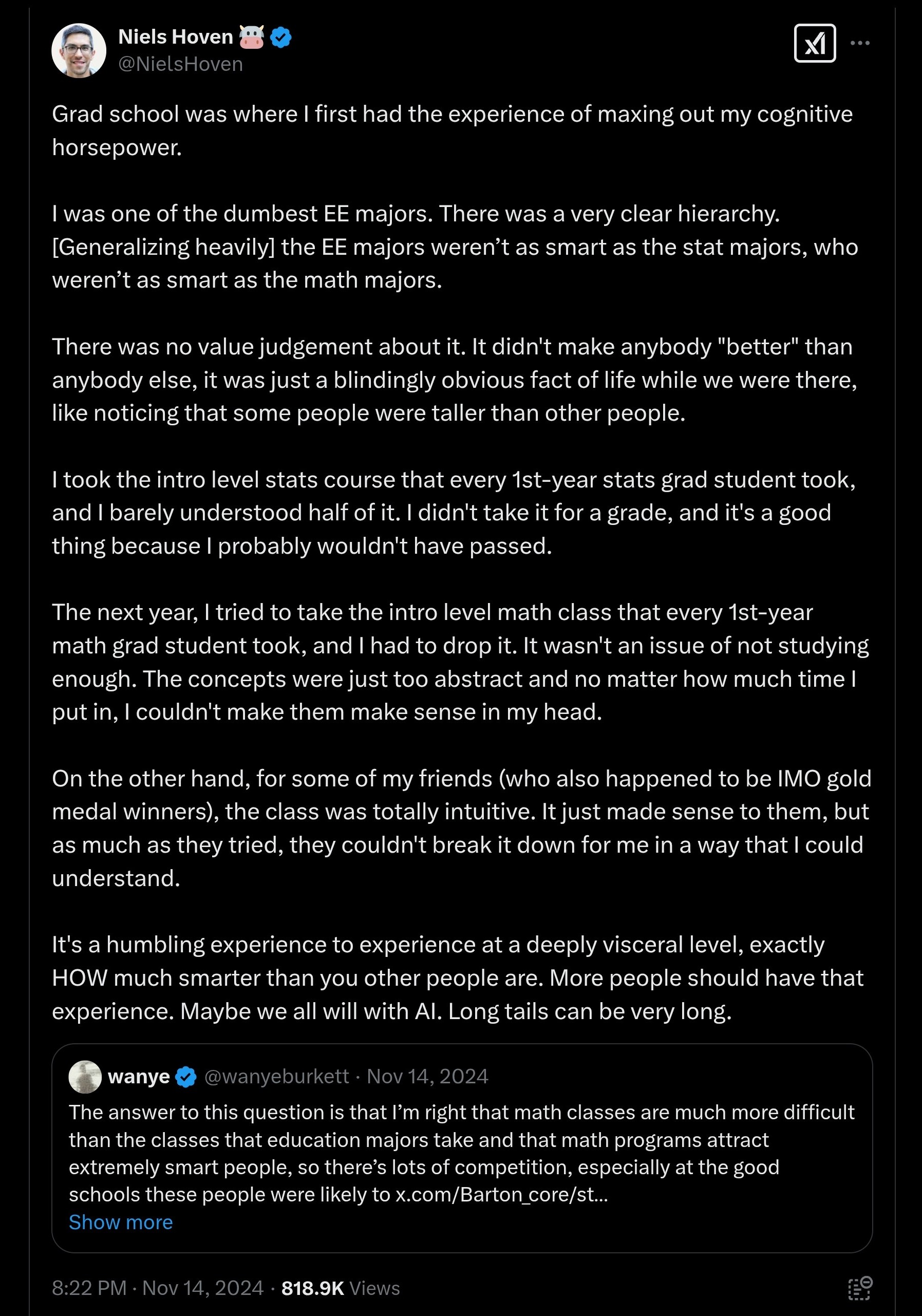image x.com/NielsHoven/status/1857232610701009099

Also, a firsthand account from Douglas Hofstadter:

  • "I am a 'mathematical person', that's for sure, having grown up profoundly in love with math and having thought about things mathematical for essentially all of my life (all the way up to today), but in my early twenties there came a point where I suddenly realized that I simply was incapable of thinking clearly at a sufficiently abstract level to be able to make major contributions to contemporary mathematics.
    ...
    I had never suspected for an instant that there was such a thing as an 'abstraction ceiling' in my head. I always took it for granted that my ability to absorb abstract ideas in math would continue to increase as I acquired more knowledge and more experience with math, just as it had in high school and in college.
    ...
    I found out a couple of years later, when I was in math graduate school, that I simply was not able to absorb ideas that were crucial for becoming a high-quality professional mathematician. Or rather, if I was able to absorb them, it was only at a snail's pace, and even then, my understanding was always blurry and vague, and I constantly had to go back and review and refresh my feeble understandings. Things at that rarefied level of abstraction ... simply didn't stick in my head in the same way that the more concrete topics in undergraduate math had ... It was like being very high on a mountain where the atmosphere grows so thin that one suddenly is having trouble breathing and even walking any longer.
    ...
    To put it in terms of another down-home analogy, I was like a kid who is a big baseball star in high school and who is consequently convinced beyond a shadow of a doubt that they are destined to go on and become a huge major-league star, but who, a few years down the pike, winds up instead being merely a reasonably good player on some minor league team in some random podunk town, and never even gets to play one single game in the majors. ... Sure, they have oodles of baseball talent compared to most other people -- there's no doubt that they are highly gifted in baseball, maybe 1 in 1000 or even 1 in 10000 -- but their gifts are still way, way below those of even an average major leaguer, not to mention major-league superstars!
    ...
    On the other hand, I think that most people are probably capable of understanding such things as addition and multiplication of fractions, how to solve linear and quadratic equations, some Euclidean geometry, and maybe a tiny bit about functions and some inklings of what calculus is about."

    -- Douglas Hofstadter (2012) in "Some Reflections on Mathematics from a Mathematical Non-mathematician"

I ran into this myself too. Around grad-level pure math I got really frustrated feeling like there was too much waxing philosophical and too few repetitions on well-scoped problems chosen to hammer in well-defined skills. Seemed like most people I ran into at that level were feeling the friction due to unfavorable practice conditions at least as severely as me, but there were a couple people for whom the miniscule level of scaffolding seemed to be enough.

It wasn’t a “hard” threshold at which I was suddenly incapable of learning more advanced pure math, but rather a “soft” threshold at which the amount of time and effort required to learn it began to skyrocket until it was effectively no longer a productive use of my time (when you consider the opportunity cost). That’s the moment I really switched over 100% to applied math and quant/algo CS.

Basically,

  • I realized that I had lost my "edge" in pure math compared to the other people I was competing with,
  • I also realized I had a knack for quantitative programming and interest in a handful of applied domains,
  • and it turned out the problems that needed solving in those domains boiled down to interesting math / algorithm development (that most people in software don't have the math chops for) plus serious coding / large-system development (that most people in math don't have the coding chops for)
  • so I pivoted in that direction where it felt like my ceiling was higher.

Chris Sutherland shared his experience as well:

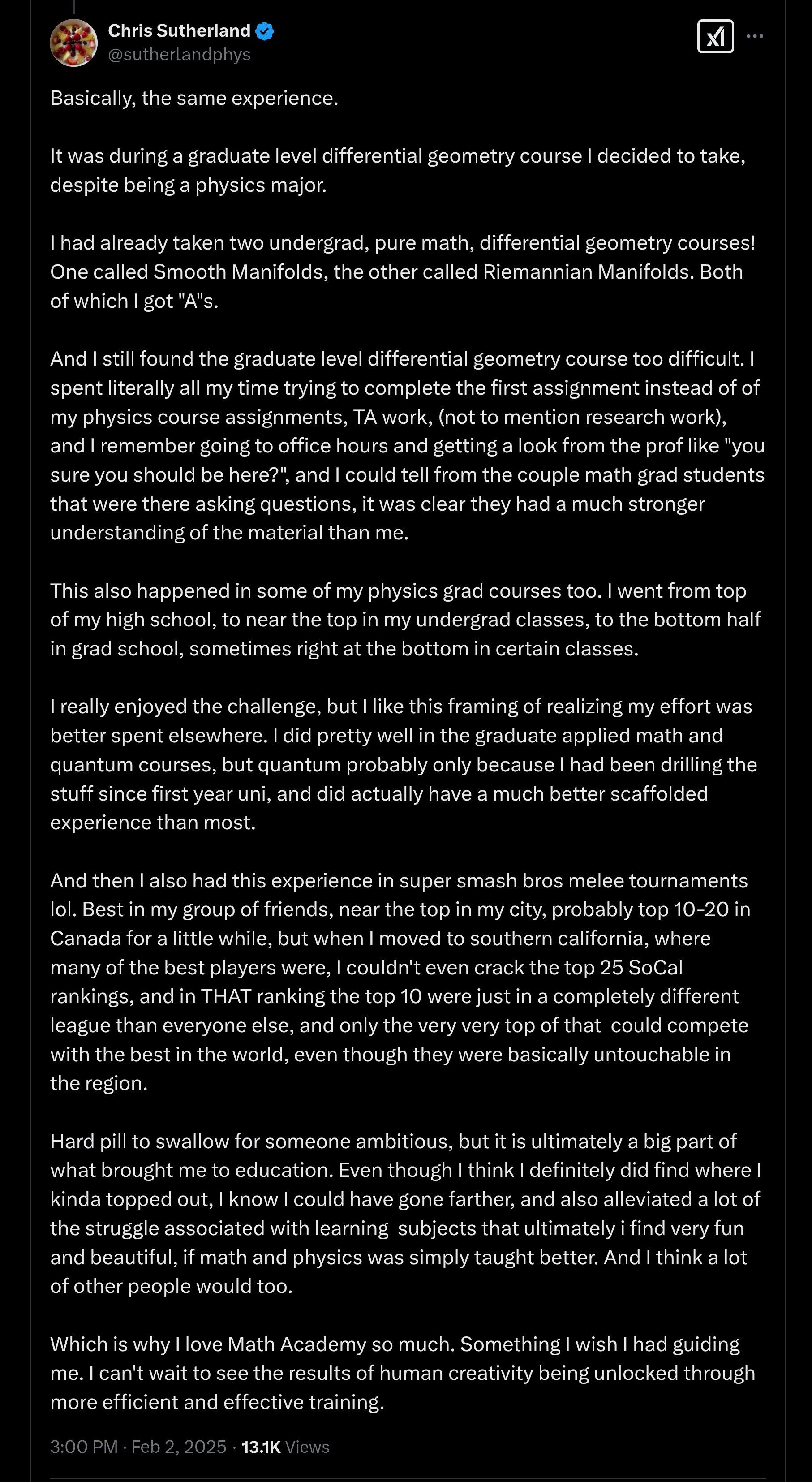image x.com/sutherlandphys/status/1886142687985725577

Basically, almost everybody who pursues serious math eventually reaches a level at which there’s just not enough scaffolding to justify continuing.

It’s not a hard threshold at which you’re suddenly incapable of learning more advanced math, but rather a soft threshold at which the amount of time and effort required to learn begins to skyrocket until it’s effectively no longer a productive use of your time (when you consider the opportunity cost).

People get off the train and stop learning math once it begins to feel too inefficient. This isn’t even a math-specific thing – the same thing plays out everywhere else in life. In anything you do, once the progress-to-work ratio gets too low, you’re going to lose interest and focus on other endeavors where your progress-to-work ratio is higher.

That’s why maximizing learning efficiency is such a big lever in maximizing student potential. Everybody who gets thrown off the learning train due to pedagogical friction could have gone further if that friction were removed. Under high-efficiency learning conditions, students not only make faster progress, but also reach higher levels of math than they would otherwise.

Learning efficiency keeps the progress-to-work ratio as high as possible, keeping students on the rails as far as possible. If that’s not the definition of maximizing student potential, I don’t know what is.

Further Reading: Your Mathematical Potential Has a Limit, but it’s Likely Higher Than You Think. Summary: While your mathematical potential has a (soft) limit, it’s likely higher than you think. Few people actually reach their full mathematical potential; they get derailed early by missing foundations, lack of scaffolding, etc.

Answers to Follow-Up Questions

How sure are you that the soft threshold is due to a lack of IQ rather than “scaffolding”?

Lack of IQ, necessity of scaffolding, these are the same thing. Cognitive advantage and instructional scaffolding are two sides of the same coin. The more cognitively advantaged you are, the less scaffolding you need to achieve a given bar for mastery in a reasonable timeframe.

(Don’t get me wrong, regardless of how high your IQ is, appropriate scaffolding will still increase your rate of learning. And by “appropriate” I mean that it adapts appropriately, you move fast with less practice required when your performance is high off the bat and slower with more practice when your performance is lower.)


Want to get notified about new posts? Join the mailing list and follow on X/Twitter.