Your Mathematical Potential Has a Limit, but it’s Likely Higher Than You Think

Not everybody can learn every level of math, but most people can learn the basics. In practice, however, few people actually reach their full mathematical potential because they get knocked off course early on by factors such as missing foundations, ineffective practice habits, inability or unwillingness to engage in additional practice, or lack of motivation.

This post is part of the book The Math Academy Way (Working Draft, Jan 2024). Suggested citation: Skycak, J., advised by Roberts, J. (2024). Your Mathematical Potential Has a Limit, but it's Likely Higher Than You Think. In The Math Academy Way (Working Draft, Jan 2024). https://justinmath.com/your-mathematical-potential-has-a-limit-but-its-likely-higher-than-you-think/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

It’s a common myth that everybody can learn every level of math.

In reality, most people can learn basic math like arithmetic and some algebra – but beyond that, higher levels of math become increasingly abstract and technical, and fewer people have the cognitive resources to learn it quickly enough to make a career out of it, much less get to that point relatively early in their lives.

Levels of Math

One problem with this myth is that most people do not understand just how deep the levels of mathematics can go, and how cognitively taxing it is to learn the deepest levels. Arithmetic is a completely different ballpark from graduate-level math (and beyond). Most people consider calculus to be “really advanced math,” but calculus is not even halfway to the level at which expert mathematicians operate.

For reference, below is a loose formulation of the levels of mathematics:

1. Arithmetic -- seldom considered "hard math"
2. Algebra -- often considered "hard math" by people who disliked math in school
3. Calculus -- considered "hard math" by the general public
4. Real Analysis, Abstract Algebra, Partial Differential Equations, etc. -- considered "hard math" by most college students majoring in math
5. Algebraic Topology, Differential Geometry, etc. -- considered "hard math" by most graduate students doing PhDs in math, as well as many research professors in math
6. The math underlying solutions to the most famous problems in modern mathematics, e.g. Ricci Flow with Surgery which underlies the proof of Poincaré Conjecture -- considered "hard math" by the world's top mathematicians

To put these levels in perspective, it can be helpful to draw an analogy to athletics:

• Learning arithmetic is like basic ambulatory movement: almost everyone can do it.
• Learning high school calculus is like being able to run ten miles without stopping: it takes time and effort to work up to it, but by training effectively and consistently, many people can accomplish it.
• Learning research-level mathematics is like qualifying for the 100-meter dash at the Olympics: it requires a certain biological predisposition coupled with the commitment of thousands of hours to the most grueling forms of training.

The reason why this is harder to accept in the context of mathematics than in the context of athletics is that we cannot observe the makeup and functioning of our brains as clearly as we can our bodies. But, as elaborated in a previous post, individual differences in brains do exist (e.g. working memory capacity) and are relevant to key mathematical skills (e.g. abstraction ability).

The Abstraction Ceiling

To help lend some concreteness to something as abstract as “abstraction ability,” it may help to hear the famed Douglas Hofstadter (2012) recount his firsthand experience of running up against an “abstraction ceiling” in his own brain while pursuing a PhD in mathematics:

As Hofstadter describes, the abstraction ceiling is not a “hard” threshold, a level at which one is suddenly incapable of learning math, but rather a “soft” threshold, a level at which the amount of time and effort required to learn math begins to skyrocket until learning more advanced math is effectively no longer a productive use of one’s time. That level is different for everyone. For Hofstadter, it was graduate-level math; for another person, it might be earlier or later (but almost certainly earlier).

Learning Energy vs Level of Math

The central insight is that the further you go in math, the more energy it requires to learn the next level up. Whether they realize it or not, everybody who learns math is on an exponential curve of energy (time and effort) versus the level of math. (A key feature of exponential curves is that they can look fairly flat at the beginning, but appear to skyrocket later on, despite there being a constant “multiplier” to get from one point to the next.)

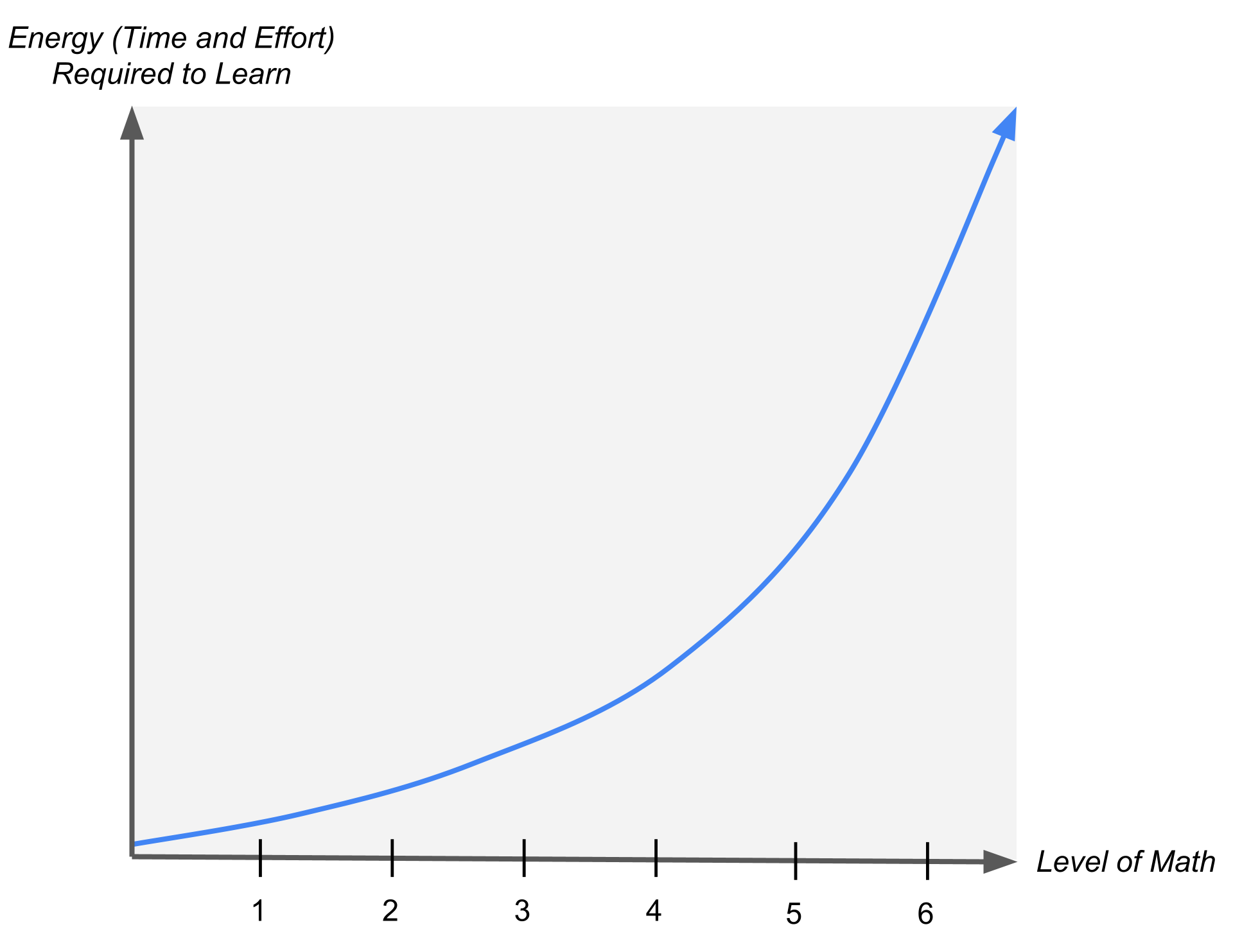
As we described in a previous post, people with lower working memory capacities generally perceive cognitive skills to require more effort and more practice to master. It is as if there is a “multiplier” on the amount of energy required.

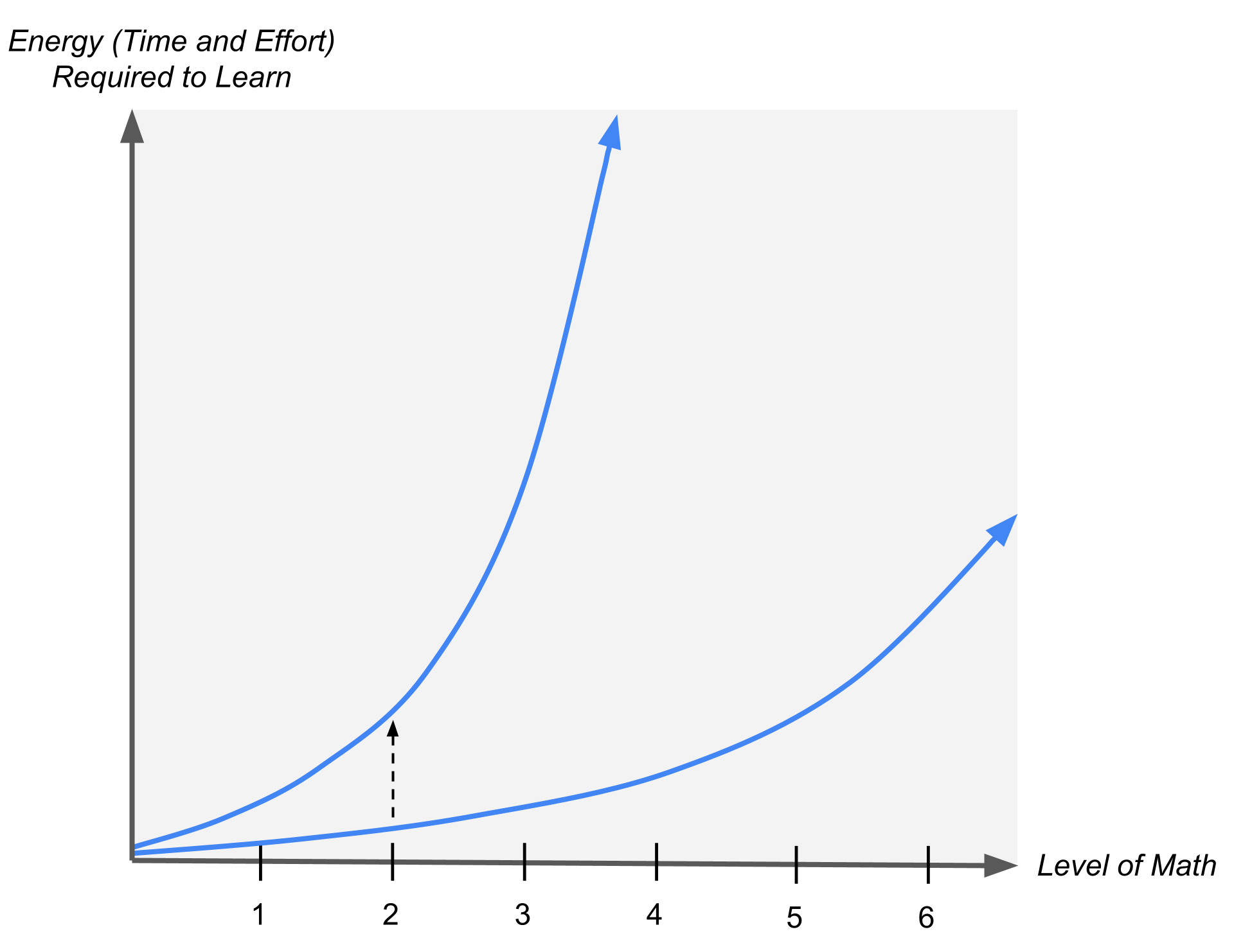
Another key feature of exponential curves is that vertical scaling is equivalent to horizontal translation. For instance, if we take the curve $2^x$ and multiply it by 8 (representing a person who requires 8 times more energy to learn math), then we have the curve $8 \cdot 2^x$ which is also equivalent to $2^{3+x},$ a horizontal shift 3 levels to the left.

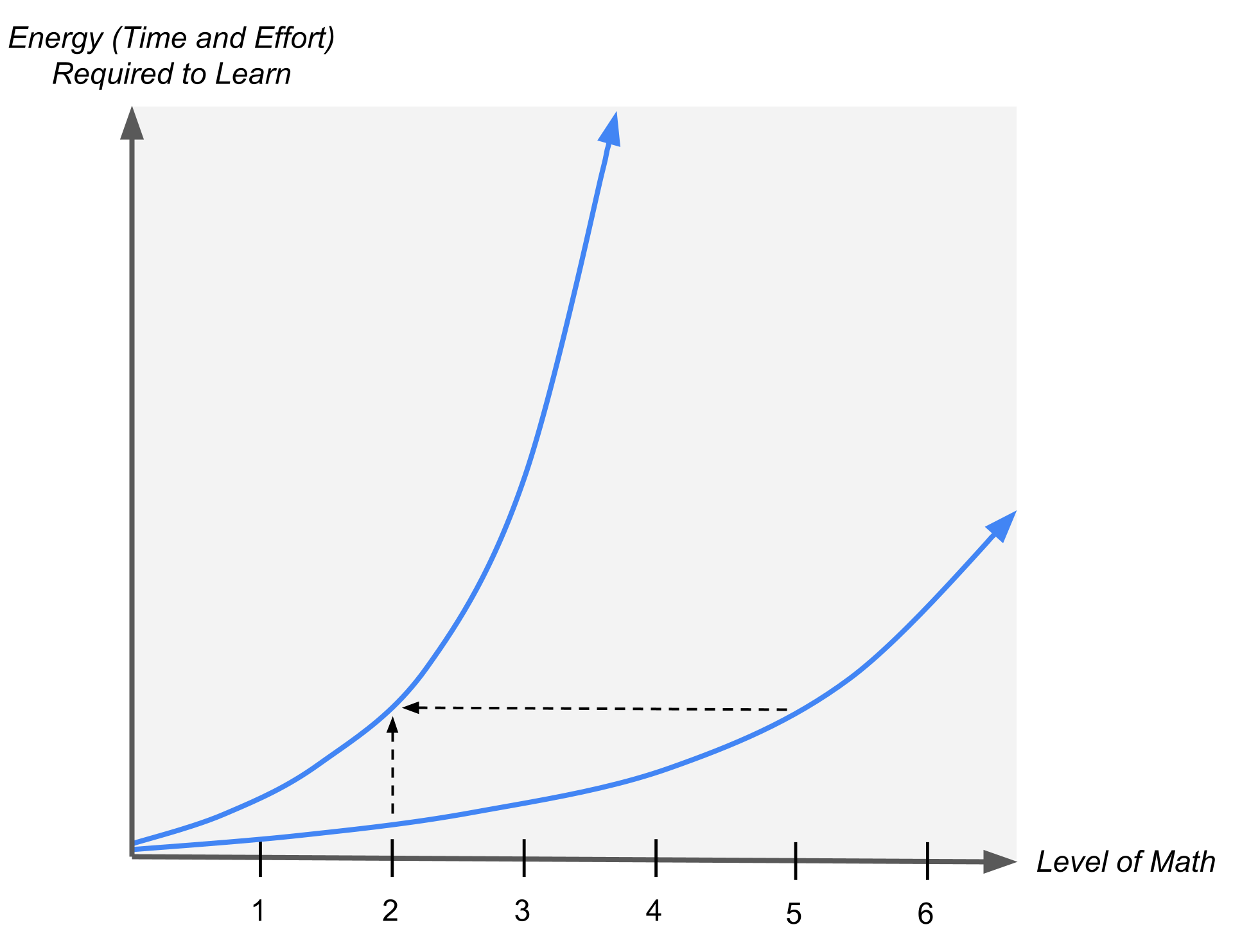
At the beginning (at the left), the two graphs are not that different, but as we look further to the right (progressively more levels of math), they quickly separate, and one graph skyrockets much earlier than the other. Everybody is on this exponential curve of energy (time and effort required to learn) versus level of abstraction, but everyone’s curve is shifted horizontally depending on their cognitive ability and degree of motivation/interest. For some people, math doesn’t get hard until graduate-level Algebraic Topology; for others, it becomes hard as early as high school algebra.

These graphs demonstrate the importance of learning efficiency: by increasing learning efficiency, one can divide the energy required to learn, flattening the graphs above, which is the same as shifting them to the right. When students enjoy high-efficiency learning conditions, they not only make faster progress, but also reach higher levels of math than they would otherwise.

Students get off the math train and stop taking math classes once it begins to feel too inefficient. Once the progress-to-work ratio gets too low, they lose interest and focus on other endeavors where their progress-to-work ratio is higher. Efficiency keeps the progress-to-work ratio as high as possible, keeping students on the math learning train for as far as possible.

All Can Learn Some, Many Can Learn More, but Few Can Learn All

Nature or Nurture? Both Matter

This characterization is compatible with the usual findings of studies into the effects of nature and nurture on skill acquisition: both matter. Talent – the top speed at which one can acquire skills in a particular domain – matters, and so does hard work. As Kirschner & Hendrick describe (2024, pp.142):

Lack of talent does not necessarily mean “you can’t do this,” but it does mean that someone lacking talent will need to work much harder, possibly to an infeasible extent, as compared to someone with talent. But because the human lifespan is so limited and human talents can be so diverse, “you need to work much harder than others to accomplish this” effectively means the same thing as “you probably won’t do this because you’ll find more efficient, productive, and fulfilling uses of your time doing other things.”

As prominent psychologist Dean Keith Simonton summarizes (2007):

Elsewhere, Simonton elaborates (2013, pp.17-26) further on the importance of both nature and nurture to the development of expert performance. It has been well established that expert performance is contingent upon favorable sociocultural conditions, family and education circumstances, and massive amounts of deliberate practice:

However, many critical traits underlying expert performance have been shown to have a significant genetic component:

While the development of expert performance depends on favorable environmental conditions and massive amounts of deliberate practice, the speed of development can be accelerated (or decelerated) by genetic factors:

Speed of Skill Acquisition Matters Because Time is Limited

Humans are subject to many real-world constraints like limited lifespans and the need to learn a marketable skill quickly enough to get a job that affords basic life amenities. Additionally, things are always competing for our attention: whenever something feels hard or uninteresting, there are many other opportunities to do things that we might find easier and at least as interesting. Consequently, we tend to be pulled in other directions once we enter a range where developing further expertise in a domain becomes overwhelmingly arduous. We switch to other things that we (often, correctly) feel are a better use of our limited time.

As prominent psychologist Robert Sternberg recounts (2014):

There are compounding factors, too: when something becomes hard and we stop doing as well, we often like it less and lose interest/motivation, which makes it even more difficult. When we are young children in school, our teachers and/or parents might force us to continue investing effort into learning specific subjects like math even when we would prefer not to, but in high school and beyond, parents and teachers are less involved in monitoring how much and how effectively we practice. As we face greater responsibilities from life in general, we are met with so many incentives to get good grades that we might shy away from taking classes that require an outsized amount of effort. All of these factors converge to pull us towards an “off ramp” when mathematics gets hard for us.

So, for all practical purposes, it is completely untrue that everyone can learn every level of math and become a research mathematician – just like it is completely untrue that anyone can become an Olympic sprinter, a professional basketball player, a world-famous comedian, a Grammy-winning singer, etc. But at the same time, almost everybody can learn basic arithmetic – just like almost everybody can learn to run, shoot a free throw, tell a joke, or hum a tune. And with proper training, most people can learn some algebra – just like most people can run a 5k, shoot a three-pointer, amuse an audience, or sing a soothing tune.

Why the "All Can Learn All" Myth Persists

There are at least two reasons why the “all can learn all” myth persists. First, the reality that “all can learn some, many can learn more, but few can learn all” can feel unfair and uncomfortable – especially in the context of mathematics, since the students who are best at math tend to be viewed as the smartest.

Second, people often overweight the importance of learning advanced math (and other technical subjects) to general success in life. In reality, lots of jobs, even those that are well-respected and lucrative, don’t require advanced math. For instance, how many doctors, lawyers, members of Congress, and even university presidents can and do use calculus in their work? Few, if any. For professions like those, advanced math is not essential. (While it may be true that a larger-than-expected minority of people in such careers may have learned advanced math at some point, knowledge of advanced math itself is typically not one of the relevant factors contributing to one’s ability to secure and maintain such a career.)

What’s important is that everyone gain basic math skills, and people with quantitative talent who are interested in math and want to go into professions that use advanced math – not just aspiring mathematicians but also aspiring physicists, bioinformaticians, rocket scientists, machine learning engineers, etc. – don’t take the “off ramp” too early and miss out on the opportunity to build a career around something they enjoy and are good at. We will address this idea more thoroughly in the next section, Struggle Does Not Imply Inability.

As a final part of debunking the current myth, it’s important to realize that even professional educators and coaches who train students are susceptible to promote the myth that anyone can do anything with a bit of hard work.

Trainers, like parents, often don’t want to tell their children that they’re not gifted/talented enough in an area to build a career out of it – which is understandable because not only does it feel mean, but it may not even be true: new and unexpected gifts/talents can emerge as a child develops.

However, for trainers in particular, there are also other incentives at play that are important to be aware of. For a trainer, there is no upside to telling a student’s parents that their child is not gifted/talented enough in an area to build a career out of it. It just makes parents and students really upset (even though professional trainers are probably correct more often than not) and, in the context of private training, often leads to loss of business. So, trainers are incentivized to avoid this treacherous territory and instead take one of the following false positions:

1. Gifts/talents are meaningless and anyone can do anything with a bit of hard work.
2. Gifts/talents are important, but there is no way to know whether a gift/talent might emerge as a young student develops, so there is no use basing any sort of decision around them.

Earlier discussion (in this post) has estabilished that the first position cannot be held rationally. However, believing in it can feel so empowering, and in turn so convincing, that it can be an effective position for a trainer to take to keep students and parents happy.

Likewise, in the second position, while it is true that even professional trainers don’t know with absolute certainty how their students (especially young students) will develop over time, they do generally have some or even a lot of information about whether a student has a gift/talent – and if not, then how likely it is that the gift/talent might emerge later in the child’s development. Leveraging that information can be a critical part of helping a child enter an area where they have both the gifts/talents and the level of interest to eventually build a career that they enjoy.

Struggle Does Not Imply Inability

Another common myth is that if you do poorly in a math class, it means you are incapable of learning that level of math.

In reality, if you do poorly in a math class, it doesn’t necessarily mean that you are incapable of learning that level of math. There are a number of reasons that could be the root cause of your struggle. While it’s true that everyone’s mathematical potential has a limit, in practice the ceilings we hit rarely represent our true “abstraction ceiling” as described by Hofstadter. All sorts of factors can artificially lower our ceilings, such as missing foundations, ineffective practice habits, inability or unwillingness to engage in additional practice, or lack of motivation.

Struggle Can Be Caused by Missing Foundations

When people age, they accumulate biological damage that eventually reaches a tipping point and leads to a cascade of catastrophic health issues. The same thing happens to students learning mathematics.

Students accumulate weaknesses and knowledge gaps as they progress through math – even a grade of B+ or A- means that there are things in the course that the student never completely grasped, much less mastered. Additionally, gaps can be created if a student takes a course that is not comprehensive and does not cover some topics that are assumed to be prior knowledge in higher-level courses. Once a student has accumulated a critical number of gaps (and by the way, a gap begets more gaps), then the student is doomed to struggle unless proper remediation is enacted to fill in those gaps.

Remediation is extremely difficult to accomplish outside the context of an adaptive, automated learning system. It rarely happens in the classroom – teachers just don’t have the bandwidth to spend enough time with each student to figure out exactly which pieces of foundational knowledge are missing. And while remediation can often be performed by a skilled tutor, it generally requires many tutoring sessions over a long period of time, continuing indefinitely into the future to prevent new gaps from forming, which makes it prohibitively expensive for most families.

Students usually stop taking math classes once they amass a critical number of knowledge gaps. The usual sequence of events starts with students trying to imitate procedures cookbook-style, without really understanding what’s going on, because they can’t intuitively grasp any of the new material that they’re being taught. Soon after that, they find themselves unable to solve any problems that involve critical thinking or many steps.

It’s similar to how professional athletes usually retire not because they’re too old, but because they’ve accumulated too many injuries. As Indiana Jones once put it: “it’s not the years, it’s the mileage.” Or as math writer/cartoonist Ben Orlin humorously described, it’s the “law of the broken futon”: a single missing part can, over time, warp an entire futon and render it unusable.

Students will almost assuredly accumulate these deficits in traditional classrooms. It’s only the most gifted and motivated students who are able and willing to identify and “self-repair” their gaps on their own.

• In traditional classrooms, students often get stuck on foundational topics but are required to complete homework on more advanced topics, leading them to "scrape by" without really understanding the subject matter.
• Students also do not review material learned in previous years, and often do not even review material from the course that they're in unless they are preparing for a test. This leads them to quickly forget what they've learned, requiring re-learning scratch if and when those topics show up again in the future.
• Often, traditional courses are not even comprehensive! It's not uncommon for instructors to run out of time before the end of the year and skip sections of the textbook.

Struggle Can Be Caused by Ineffective Practice

As explained in a previous post summarizing the science of learning, effective learning feels like a workout with a personal trainer. It should center around deliberate practice, a type of active learning in which individualized training activities are specially chosen to improve specific aspects of performance through repetition and successive refinement.

Active learning and deliberate practice will be covered in more depth in later posts, but below are some key points:

• Effective learning is active, not passive. It is not effective to attempt to learn by passively watching videos, attending lectures, reading books, or re-reading notes.
• Deliberate practice requires repeatedly practicing skills that are beyond one's repertoire. However, this tends to be more effortful and less enjoyable, which can mislead non-experts to practice within their level of comfort.
• Classroom activities that are enjoyable, collaborative, and non-repetitive (such as group discussions and freeform/unstructured project-based or discovery learning) can sometimes be useful for increasing student motivation and softening the discomfort associated with deliberate practice -- but they are only supplements, not substitutes, for deliberate practice.
• Deliberate practice must be a part of a consistent routine. The power of deliberate practice comes from compounding of incremental improvements over a longer period of time. It is not a "quick fix" like cramming before an exam.

Struggle Can Be Caused by Insufficient Practice

Struggle can be caused by needing more practice than other students (or, equivalently, the pace of the class might be too fast). This is not necessarily a catastrophic issue in itself because it can usually be remedied by engaging in further practice. However, it can cause problems if coupled with other factors such as the following:

• The instructional material is not highly scaffolded.
• Few practice problems are available.
• Exam problems are substantially different from homework problems.
• The additional practice required exceeds the amount of effort that you are willing to put forth to learn the material.

Struggle Can Be Caused by Lack of Motivation

Properly motivated students are usually driven by one or more of the following factors:

• They are intrinsically interested in the material. Some students truly love math and see beauty in the way various mathematical ideas fit together and give rise to new perspectives.
• The material is highly relevant to their future goals. For instance, an aspiring rocket scientist might not love math but might be motivated to learn it because of how useful it is for getting rockets into space. Likewise, an aspiring doctor might not love math but might be required to evidence a baseline level of mathematical knowledge when applying to medical school. Even students who do not have specific future goals might feel strongly about keeping potential career doors open which would otherwise be shut by not learning enough math.
• They enjoy competing in mathematical exams and science fairs. Some students have neutral feelings about math, but find that they are good at it, and that they enjoy learning more advanced mathematics to provide a competitive edge in exams and science fairs.
• Their parents have motivated them with a meaningful extrinsic reward. Sometimes, a student may not fall into any categories above, but their parents (often rightfully so) want them to fully take advantage of any opportunities to learn math while they are still in school. For some students, this may mean learning the basic math they need to get by in life after school; for other students, this may mean learning more advanced math to open a wide variety of career doors. If a student is highly interested in other activities like reading novels, playing video games, or even something as simple as going out for dessert, offering them extrinsic rewards in return for meeting checkpoints in their math learning can often provide sufficient motivation to keep them from "checking out" during learning.

If a student is not driven by any of the motivational factors above, they may “check out” or otherwise struggle due to a lack of interest in learning the material.

Analogy to Lifespans

The key takeaway from this post is that your mathematical potential has a limit, but it’s likely higher than you think. If this idea still feels unclear, then it may help to draw an analogy to human lifespans.

Your lifestyle will affect the length of your life, but even if you live perfectly healthily, there is no guarantee that you will become a supercentenarian (110+ years old). A tiny fraction of people will live that long, but probably not you, even if you do everything right. However, it is still true that you can vastly extend your lifespan if you live healthily, as compared to if you live unhealthily.

The same is true in athletics. Even if you practice effectively for longer than anyone else, there is no guarantee that you will become a hall-of-fame athlete. However, it is still true that you will become vastly more skilled in your chosen sport than if you practiced ineffectively or didn’t put in as much time. Quite likely, you will become more skilled than you or anyone else thought was possible.

Mathematics is no different. Even if you devote your life to effective study, there is no guarantee that you will become a world-class mathematician. But by putting a serious effort into effective study, you will learn far more math and open far more career doors than you would otherwise.

Student Bite Size vs Curriculum Portion Size

Thinking deeply about the role of instruction in supporting learners, it’s possible to arrive at the following misconception.

The Misconception: If Instruction is Done Perfectly, Won’t All Students Learn at the Same Rate?

Higher math is heavily g-loaded, which creates a cognitive barrier for many students. The goal of instructional scaffolding, guidance, and review is to help boost students over that barrier.

But if the purpose of scaffolding, guidance, and review is to help students overcome cognitive blockers, then wouldn’t a theoretical learning environment with infinite scaffolding, guidance, and review completely factor out cognitive differences, causing students to learn at the same rate?

Sure, the speed at which students learn (and remember what they’ve learned) varies from student to student. It has been shown that some students learn faster and remember longer, while other students learn slower and forget more quickly (e.g., Kyllonen & Tirre, 1988; Zerr et al., 2018; McDermott & Zerr, 2019).

But perhaps these studies are simply reflective of unfavorable learning conditions, and people would learn at the same rate in an optimally favorable learning environment?

The Resolution: Under Favorable Learning Conditions, Student Bite Size Equals Curriculum Portion Size

Continuing to think deeply about this thought experiment, one will eventually realize that infinite scaffolding, guidance, and review is not synonymous with optimally favorable learning conditions.

Sure, students will eat meals of information at similar bite rates when each spoonful fed to them is infinitesimally small. However, “eating at the same rate” would be a ceiling effect.

Faster learners would be capable of learning faster, but the curriculum would be too granular relative to their generalization ability and/or provide too much review relative to their forgetting rate, thereby creating a ceiling effect that prevents fast learners from learning at their top speed.

A maximally-favorable learning environment would require that the curriculum’s granularity is equal to the student’s bite size and the rate of review is equal to the student’s rate of forgetting.

The amended metaphor: Students eat meals of information at similar bite rates when each spoonful fed to them is sized appropriately relative to the size of their mouth.

This type of learning environment would maximize each student’s individual potential, free of ceiling effects. Critically, however, students would not progress through it at the same rate: equal bite rates does not imply equal rates of food volume intake.

Consistency with Observations

This framing of favorable learning conditions (“student bite size equals curriculum portion size”) is consistent with the phenomenon that math becomes hard for different students at different levels. The following factors affect students differentially as they move up the levels of math:

• Combinatorial explosion in the problem space -- lowers the "bite size" more for students with lower generalization ability, or, equivalently, reduces the perceived granularity of the curriculum. (This may be a contributing factor in cases when, e.g., students do fine in math but struggle in physics.)
• Large body of knowledge to maintain -- increases the amount of review more for students with higher forgetting rates. Also reduces effective "bite size" since an increasing portion of each bite will consist of reviewing fuzzy prerequisite material.

It is also consistent with the concept of soft and hard ceilings on the highest level of math that one can reach:

• Say we have a student with low generalization ability and high forgetting rate. Then a favorable curriculum takes more time to work through (as compared to a favorable curriculum for an average student) due to increased granularity and review, and that multiplier increases as they go up the levels of math.
• At some point "it requires lots of practice to learn" becomes synonymous with "can't learn" -- first in a soft sense of "the benefits of engaging in this much practice do not outweigh the opportunity costs of neglecting to develop my skills in other domains that I find easier," and then in a hard sense of "the amount of practice required exceeds the sum of waking hours over the remainder of my life."

References

Hofstadter, D., & Carter, K. (2012). Some Reflections on Mathematics from a Mathematical Non-mathematician. Mathematics in School, 41(5), 2-4.

Kirschner, P., & Hendrick, C. (2024). How learning happens: Seminal works in educational psychology and what they mean in practice. Routledge.

Kyllonen, P. C., & Tirre, W. C. (1988). Individual differences in associative learning and forgetting. Intelligence, 12(4), 393-421.

McDermott, K. B., & Zerr, C. L. (2019). Individual differences in learning efficiency. Current Directions in Psychological Science, 28(6), 607-613.

Simonton, D. K. (2007). Talent and expertise: The empirical evidence for genetic endowment. High Ability Studies, 18(1), 83-84.

Simonton, D. K. (2013). If innate talent doesn’t exist, where do the data disappear?. The complexity of greatness: Beyond talent or practice, 17-26.

Sternberg, R. J. (2014). Costs of expertise. In The road to excellence (pp. 347-354). Psychology Press.

Zerr, C. L., Berg, J. J., Nelson, S. M., Fishell, A. K., Savalia, N. K., & McDermott, K. B. (2018). Learning efficiency: Identifying individual differences in learning rate and retention in healthy adults. Psychological science, 29(9), 1436-1450.

This post is part of the book The Math Academy Way (Working Draft, Jan 2024). Suggested citation: Skycak, J., advised by Roberts, J. (2024). Your Mathematical Potential Has a Limit, but it's Likely Higher Than You Think. In The Math Academy Way (Working Draft, Jan 2024). https://justinmath.com/your-mathematical-potential-has-a-limit-but-its-likely-higher-than-you-think/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.