Recreational Mathematics: Why Focus on Projects Over Puzzles

There's only so much you can hone your math skills by working on a problem that someone else has intentionally set up to be well-posed and elegantly solvable if you think about it the right way.

Cross-posted from here.

Personally, my most enjoyable and productive mathematical experiences while growing came from toy research projects. Some examples:

• When I learned about partial fractions decomposition in high school, I wondered if I could come up with a formula for the coefficients $c_{jk}$ in the partial fractions expression of
  
  $\begin{align*} \dfrac{b_0 + b_1 x_1 + b_2 x_2 + \cdots + b_n x^n}{(x-a_1)^{k_1} (x-a_2)^{k_2} \cdots (x-a_m)^{k_m}} = \sum_{j=1}^m \sum_{k=1}^{k_j} \dfrac{c_{jk}}{(x-a_j)^k} \end{align*}$
  by writing down and solving the system of equations in the general case, and also conducting numerical experiments to look for relevant patterns that I could prove and leverage in helpful ways. This turned out to be a very difficult and messy project but I did obtain one reasonably neatly-packaged result,
  
  $\begin{align*} \dfrac{x^n}{(x-a)^k} = \sum_{i=0}^{n-k} \binom{n-1-i}{k-1} a^{n-k-i} x^i + \sum_{i=\max(k-n,1)}^k \dfrac{\binom{n}{k-i} a^{n-k+i}}{(x-a)^i}, \end{align*}$
  and proving it gave me my first experience with double-induction.
• In my first year of college I got interested in neuroscience and I wondered if it was possible to, given a network of neurons, work out how the network's connectivity will change if you pick one neuron and repeatedly "activate" it with a pulse that ripples through the network. (Whenever two neurons activate, the connection strength between them changes according to known biological learning rules -- the simplest and earliest-discovered rule is "what fires together wires together," known as Hebbian learning, but since then more nuanced rules have been discovered like spike-timing-dependent plasticity, which takes temporal directionality into account.)
  
  Similar to the previous problem, my approach was again a combination of working out math by hand and also running computer simulations to look for helpful patterns. The problem was again very difficult and messy, but again I really leveled up my skills by grappling with it and I discovered plenty of interesting things along the way.
  
  
  

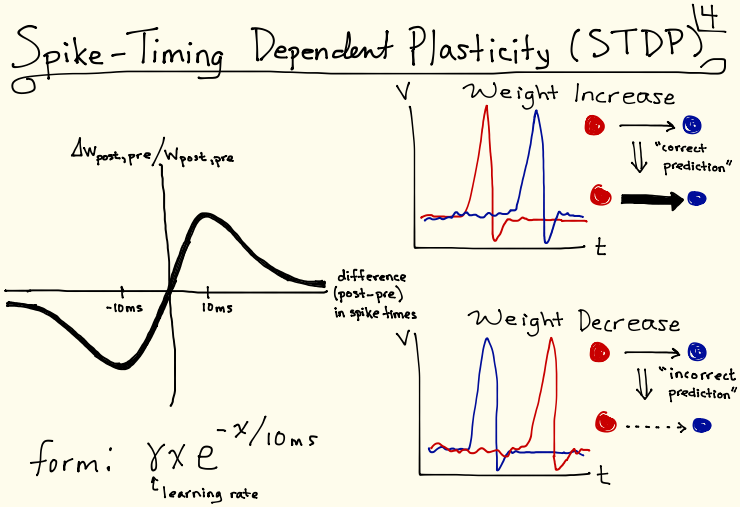
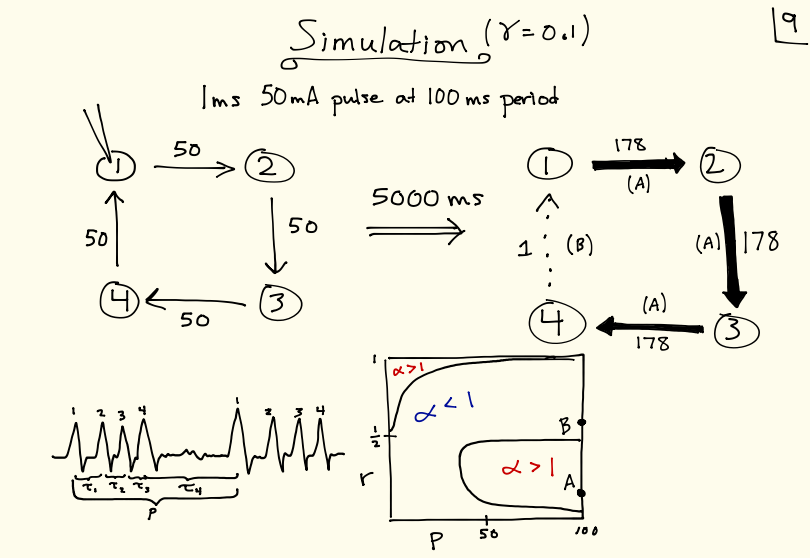
More info about these and a ton of other projects can be found here: justinmath.com/old-projects

They were a lot of hard work, and I can’t say that any of them were academically successful in the sense of yielding publishable results, but boy did they level up my mathematical ability more than any puzzle or textbook exercise – not just my pure mathematical reasoning ability, but also my general ability to wield math as a weapon to fight against really hard problems.

That’s the thing about research projects versus puzzles. There’s only so much you can hone your math skills by working on a problem that someone else has intentionally set up to be well-posed and elegantly solvable if you think about it the right way. You’re in a sandbox, and the problems that you fight against have been artificially handicapped to be weak opponents. It’s perfectly reasonable for beginners to start here, but people often continue training in that sandbox for way too long and then come out expecting to conquer the world. And then they’re faced with the rude awakening that they’re actually really weak against problems that have not been artificially subdued.