Tests for Convergence

by Justin Skycak (@justinskycak) on

Various tricks for determining whether a series converges or diverges.

This post is part of the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). Tests for Convergence. In Justin Math: Calculus. https://justinmath.com/tests-for-convergence/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Previously, we saw that sum formulas are only valid for series that converge. But how can we tell whether a series converges or diverges, in the first place?

Trivial Test

First of all, an easy way to tell that a series diverges is to look at the terms of the series – if the terms themselves do not converge to $0$, then their sum cannot possibly converge.

But if the terms do converge to $0$, then we can’t tell whether the series converges or diverges, and we have to use a more powerful test.

Integral Test

The integral test is a powerful test for proving convergence. It says that if the series can be written as $f(1) + f(2) + f(3) + \ldots$ for some decreasing function $f$, then the series converges if the integral $\int_1^\infty f(x) \, dx$ converges, and diverges if the integral $\int_1^\infty f(x) \, dx$ diverges.

For example, to tell whether the series

$\begin{align*} 1 + \frac{1}{2} + \frac{1}{3} + \ldots \end{align*}$


conveges, we can perform the integral test with $\int_1^\infty \frac{1}{x} \, dx$. This integral diverges to infinity, so the series above diverges to infinity as well.

$\begin{align*} \int_1^\infty \frac{1}{x} \, dx &= \left[ \ln x \right]_1^\infty \\ &= \ln \infty - \ln 1 \\ &= \infty - 0 \\ &= \infty \end{align*}$


On the other hand, applying the integral test to the series

$\begin{align*} 1+ \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \ldots \end{align*}$


shows that the series converges. (But the series does not converge to the same value of the integral – the integral test can tell us that a series converges, but not the value to which it converges. In general, the value to which a series converges may be difficult to compute.)

$\begin{align*} \int_1^\infty \frac{1}{x^2} \, dx &= \left[ -\frac{1}{x} \right]_1^\infty \\ &= -\frac{1}{\infty} - \left( -\frac{1}{1} \right) \\ &= 0-(-1) \\ &= 1 \end{align*}$


More generally, considering all exponents in the denominator, we can use the integral test to show that any series of the form

$\begin{align*} \frac{1}{1^p} + \frac{1}{2^p} + \frac{1}{3^p} + \ldots \end{align*}$


converges when $p>1$ (and diverges otherwise).

Derivation of the Integral Test

The integral test works because the value of the integral is bounded above by the series, and below by the series excluding the first term.

$\begin{align*} f(2) + f(3) + f(4) + \ldots < \int_1^\infty f(x) \, dx < f(1) + f(2) + f(3) + \ldots \end{align*}$


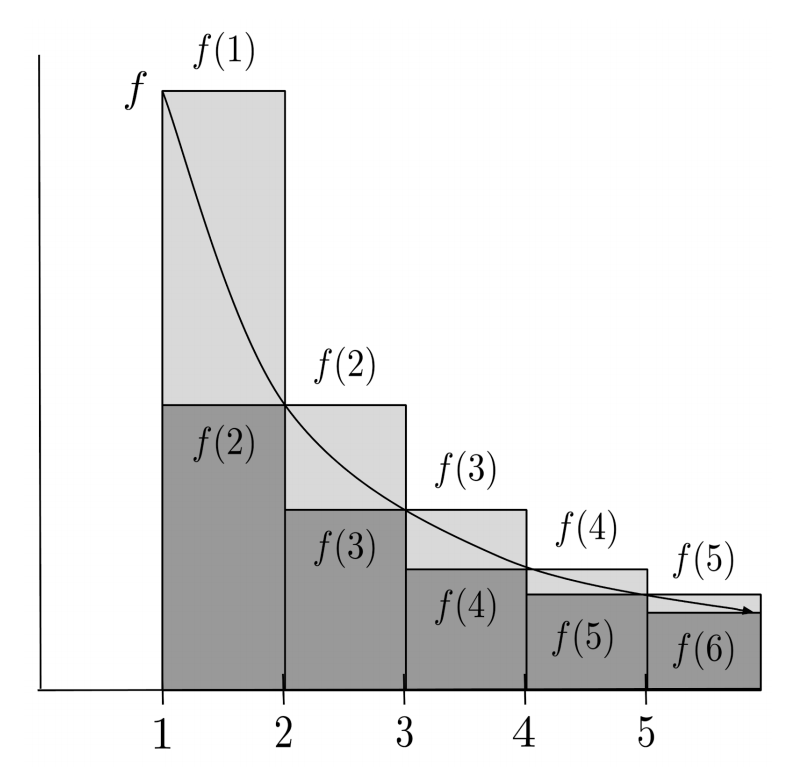
image


If the integral converges, then the series excluding the first term must converge, and adding a single finite term to the series cannot affect convergence, so the series in full must converge.

On the other hand, if the integral diverges, then since the series is greater than the integral, the series must also diverge.

Ratio Test

Another powerful test for proving convergence is the ratio test, which does not require any integration and thus can handle hard-to-integrate series.

The ratio test says that if the ratio of terms in a series has a limit $r$, then the series is almost like a geometric series with ratio $r$ – it converges if $|r|<1$, and diverges if $|r|>1$. The only catch is that if $r=1$, then we can’t tell whether the series converges or diverges (whereas a geometric series with $r=1$ must diverge).

For example, consider the following series:

$\begin{align*} 3 + \frac{9}{2!} + \frac{27}{3!} + \frac{81}{4!} + \ldots \end{align*}$


The $\text{n}^\text{th}$ term of this series is given by $\frac{3^n}{n!}$, and the ratio of the terms has a limit of $0$, so the ratio test tells us that the series converges.

$\begin{align*} \lim\limits_{n\to \infty} \frac{\frac{3^{n+1}}{(n+1)!} }{\frac{3^n}{n!} } &= \lim\limits_{n \to \infty} \frac{n! \cdot 3^{n+1} }{(n+1)! \cdot 3^n } \\ &= \lim\limits_{n \to \infty} \frac{3}{n+1} \\ &= 0 \end{align*}$


On the other hand, the $\text{n}^\text{th}$ term of the series

$\begin{align*} -\frac{1}{10} + \frac{2!}{10^2} - \frac{3!}{10^3} + \frac{4!}{10^4} - \ldots \end{align*}$


is given by $\frac{n! \cdot (-1)^n}{10^n}$, and the ratio of the terms has a limit that diverges to $-\infty$, so the ratio test tells us that the series diverges.

$\begin{align*} \lim\limits_{n\to \infty} \frac{ \frac{(n+1)! \cdot (-1)^{n+1} }{10^{n+1} } }{ \frac{n! \cdot (-1)^n}{10^n} } &= \lim\limits_{n\to\infty} \frac{(n+1)! \cdot (-1)^{n+1} \cdot 10^n}{n! \cdot (-1)^n \cdot 10^{n+1} } \\ &= \lim\limits_{n\to\infty} \frac{(n+1) \cdot (-1)}{10} \\ &= \lim\limits_{n\to\infty} -\frac{n+1}{10} \\ &= -\infty \end{align*}$


Root Test

Yet another test for convergence, called the root test, says that if the $\text{n}^\text{th}$ root of the $\text{n}^\text{th}$ term of the series has a limit $r$, then it is (once again) almost like a geometric series with ratio $r$ – it converges if $|r|<1$, and diverges if $|r|>1$. The only catch (once again) is that if $r=1$, then we can’t tell whether the series converges or diverges.

For example, consider the following series:

$\begin{align*} 1 + \left( \frac{2}{3} \right)^4 + \left( \frac{3}{5} \right)^6 + \left( \frac{4}{7} \right)^8 + \ldots \end{align*}$


The $\text{n}^\text{th}$ term of this series is given by $\left( \frac{n}{2n-1} \right)^{2n}$, and the $\text{n}^\text{th}$ root of the $\text{n}^\text{th}$ term has a limit of $\frac{1}{4}$, so the root test tells us that the series converges.

$\begin{align*} \lim\limits_{n\to \infty} \left[ \left( \frac{n}{2n-1} \right)^{2n} \right]^\frac{1}{n} &= \lim\limits_{n \to \infty} \left( \frac{n}{2n-1} \right)^2 \\ &= \left( \lim\limits_{n \to \infty} \frac{n}{2n-1} \right)^2 \\ &= \left( \frac{1}{2} \right)^2 \\ &= \frac{1}{4} \end{align*}$


On the other hand, the $\text{n}^\text{th}$ term of the series

$\begin{align*} \frac{1}{5^3} + \frac{2^2}{5^6} + \frac{3^3}{5^9}+ \frac{4^4}{5^{12}} + \ldots \end{align*}$


is given by $\frac{n^n}{5^{3n}}$, and the $\text{n}^\text{th}$ root of the $\text{n}^\text{th}$ term has a limit that diverges to infinity, so the root test tells us that the series diverges.

$\begin{align*} \lim\limits_{n\to \infty} \left[ \frac{n^n}{5^{3n} } \right]^\frac{1}{n} &= \lim\limits_{n \to \infty} \frac{n}{5^{3} } \\ &= \infty \end{align*}$


Limit Comparison Test

Lastly, the limit comparison test tells us that for any series $a_1+a_2+a_3+\ldots$, if we create another series $b_1+b_2+b_3+\ldots$ such that $\lim\limits_{n\to \infty} \frac{a_n}{b_n} = c$ for some positive constant $c$, then either both series converge or both series diverge.

The limit comparison test can simplify the process of finding convergence for complicated series – for example, given a series with terms $\frac{n+\sin n}{n}$, we can construct a new series with terms $\frac{1}{n}$ whose ratio with the original series has a limit of $1$.

$\begin{align*} \lim\limits_{n\to\infty} \frac{ \frac{n+\sin n}{ n^2} }{ \frac{1}{n} } &= \lim\limits_{n\to\infty} \frac{n+\sin n}{n} \\ &= \lim\limits_{n\to\infty} \left[ 1 + \frac{\sin n}{n} \right] \\ &= 1 + 0 \\ &= 1 \end{align*}$


Since the series with terms $\frac{1}{n}$ diverges, the original series with terms $\frac{n+\sin n}{n^2}$ must diverge as well.

Likewise, the series with terms $\frac{3n+2}{ \sqrt{n^6+1} }$ can be compared to the series with terms $\frac{1}{n^2}$.

$\begin{align*} \lim\limits_{n\to\infty} \frac{ \frac{3n+2}{\sqrt{n^6+1}} }{ \frac{1}{n^2} } &= \lim\limits_{n\to\infty} \frac{3n^3+2n^2}{\sqrt{n^6+1}} \\ &= \lim\limits_{n\to\infty} \sqrt{\frac{(3n^3+2n^2)^2}{n^6+1} } \\ &= \lim\limits_{n\to\infty} \sqrt{\frac{9n^6+12n^5+4n^4}{n^6+1} } \\ &= \sqrt{ \lim\limits_{n\to\infty} \frac{9n^6+12n^5+4n^4}{n^6+1} } \\ &= \sqrt{9} \\ &= 3 \end{align*}$


We know the series with terms $\frac{1}{n^2}$ converges, so the original series with terms $\frac{3n+2}{ \sqrt{n^6+1} }$ must converge as well.

Exercises

Tell whether each series converges or diverges. (You can view the solution by clicking on the problem.)

$\begin{align*} 1) \hspace{.5cm} \sum\limits_{n=1}^\infty \frac{2n}{n^2-4} \end{align*}$
Solution:
$\begin{align*} \text{diverges} \end{align*}$


$\begin{align*} 2) \hspace{.5cm} \sum\limits_{n=1}^\infty \frac{4}{(3n-2)^2} \end{align*}$
Solution:
$\begin{align*} \text{converges} \end{align*}$


$\begin{align*} 3) \hspace{.5cm} \sum\limits_{n=1}^\infty \frac{\ln (n^2)}{n^2} \end{align*}$
Solution:
$\begin{align*} \text{converges} \end{align*}$


$\begin{align*} 4) \hspace{.5cm} \sum\limits_{n=1}^\infty ne^{-n} \end{align*}$
Solution:
$\begin{align*} \text{converges} \end{align*}$


$\begin{align*} 5) \hspace{.5cm} \sum\limits_{n=1}^\infty (n!) e^{-n} \end{align*}$
Solution:
$\begin{align*} \text{diverges} \end{align*}$


$\begin{align*} 6) \hspace{.5cm} \sum\limits_{n=1}^\infty \frac{e^{n^2} }{n!} \end{align*}$
Solution:
$\begin{align*} \text{diverges} \end{align*}$


$\begin{align*} 7) \hspace{.5cm} \sum\limits_{n=1}^\infty \frac{n!}{(2n)!} \end{align*}$
Solution:
$\begin{align*} \end{align*}$


$\begin{align*} 8) \hspace{.5cm} \sum\limits_{n=1}^\infty \frac{n}{2^n} \end{align*}$
Solution:
$\begin{align*} \text{converges} \end{align*}$


$\begin{align*} 9) \hspace{.5cm} \sum\limits_{n=1}^\infty \frac{1}{\left( \ln n \right)^n} \end{align*}$
Solution:
$\begin{align*} \text{converges} \end{align*}$


$\begin{align*} 10) \hspace{.5cm} \sum\limits_{n=1}^\infty \left( \frac{n}{2n+1} \right)^\frac{n}{2} \end{align*}$
Solution:
$\begin{align*} \text{converges} \end{align*}$


$\begin{align*} 11) \hspace{.5cm} \sum\limits_{n=1}^\infty \left( \frac{1-9n}{1-2n} \right)^n \end{align*}$
Solution:
$\begin{align*} \text{diverges} \end{align*}$


$\begin{align*} 12) \hspace{.5cm} \sum\limits_{n=1}^\infty \left( \frac{1}{2} + \frac{1}{n} \right)^n \end{align*}$
Solution:
$\begin{align*} \text{converges} \end{align*}$


$\begin{align*} 13) \hspace{.5cm} \sum\limits_{n=1}^\infty \frac{n^2-n}{n^3+1} \end{align*}$
Solution:
$\begin{align*} \text{diverges} \end{align*}$


$\begin{align*} 14) \hspace{.5cm} \sum\limits_{n=1}^\infty \frac{n+8}{ \sqrt{n^5+2} } \end{align*}$
Solution:
$\begin{align*} \text{converges} \end{align*}$


$\begin{align*} 15) \hspace{.5cm} \sum\limits_{n=1}^\infty \frac{n^3-n+2}{(n+4)^2} \end{align*}$
Solution:
$\begin{align*} \text{diverges} \end{align*}$


$\begin{align*} 16) \hspace{.5cm} \sum\limits_{n=1}^\infty \frac{n+1}{ne^n} \end{align*}$
Solution:
$\begin{align*} \text{converges} \end{align*}$


This post is part of the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). Tests for Convergence. In Justin Math: Calculus. https://justinmath.com/tests-for-convergence/


Want to get notified about new posts? Join the mailing list and follow on X/Twitter.