Span, Subspaces, and Reduction

The span of a set of vectors consists of all vectors that can be made by adding multiples of vectors in the set. We can often reduce a set of vectors to a simpler set with the same span.

This post is part of the book Justin Math: Linear Algebra. Suggested citation: Skycak, J. (2019). Span, Subspaces, and Reduction. In Justin Math: Linear Algebra. https://justinmath.com/span-subspaces-and-reduction/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

The span of a set of vectors consists of all vectors that can be made by adding multiples of vectors in the set.

For example, the span of the set $\left\lbrace \left< 1,0 \right>, \left< 0,1 \right> \right\rbrace$ is just the entirety of the 2-dimensional plane: any vector $\left< x,y \right>$ in this plane can be made by adding $x \left< 1,0 \right> + y \left< 0,1 \right>$. For instance, $\left< 5,-2 \right>$ can be written as $5\left< 1,0 \right> - 2 \left< 0,1 \right>$.

Similarly, the span of the set $\left\lbrace \left< 1,1 \right>, \left< -1,1 \right> \right\rbrace$ is also the entirety of the 2-dimensional plane: any vector $\left< x,y \right>$ in this plane can be made by adding $\left( \frac{x+y}{2} \right) \left< 1,1 \right> + \left( \frac{x-y}{2} \right) \left< 1,-1 \right>$. This is a little less obvious, but it’s true: for example, $\left< 3,-7 \right>$ can be written as $-2 \left< 1,1 \right> + 5 \left< 1,-1 \right>$.

The span of the set $\left\lbrace \left< 1,1 \right>, \left< 2,2 \right> \right\rbrace$, however, is just a 1-dimensional line within the 2-dimensional plane: it contains only vectors of the form $k\left< 1,1 \right>$, where $k$ is a constant. To see why this is, observe what happens when we try to add multiples of the vectors:

Subspaces of Two-Dimensional Space

The span of $\left\lbrace \left< 1,1 \right>, \left< 2,2 \right> \right\rbrace$ is a 1-dimensional line within the 2-dimensional plane. So, we say that the span forms a 1-dimensional subspace of the 2-dimensional plane.

In 2 dimensions, it turns out that any set of two vectors that are multiples of one another will span a line, and any set of two vectors that are NOT multiples of one another will span the entire space.

For example, the set $\left\lbrace \left< 2,-3 \right>, \left< -4,6 \right> \right\rbrace$ spans a line because $\left< -4,6 \right> = -2 \left< 2,-3 \right>$. On the other hand, the set $\left\lbrace \left< 7,4 \right>, \left< 1,-2 \right> \right\rbrace$ spans the entire space because the vectors cannot be written as multiples of each other.

But just because two vectors are multiples, doesn’t mean they can’t be included in a set that spans the space. For example, the set $\left\lbrace \left< 1,1 \right>, \left< 2,2 \right> \right\rbrace$ spans only a line, but if we add include a third vector $\left< 1,2 \right>$ that is not a multiple of the original two vectors, then the set $\left\lbrace \left< 1,1 \right>, \left< 2,2\right>, \left< 1,2 \right> \right\rbrace$ spans the entire plane.

Subspaces of N-Dimensional Space

Now, let’s generalize these ideas to N dimensions. It might be tempting to think that in general, a set of vectors will span the entire space provided there are some three vectors that aren’t multiples of one another. But this isn’t always true.

For example, consider the set $\left\lbrace \left< 1,0,0 \right>, \left< 0,1,0 \right>, \left< 1,1,0 \right> \right\rbrace$. None of these vectors are multiples of each other, but there is no way to combine the vectors to reach a point whose third component is not zero.

The issue here is that the third vector is the sum of the first two vectors. As a result, the third vector is redundant – we can already reach any point using the first two vectors, that we can reach using the third vector. The set, then, has the same span as the set of just the first two vectors. It covers just a plane, a 2-dimensional subspace of 3-dimensional space.

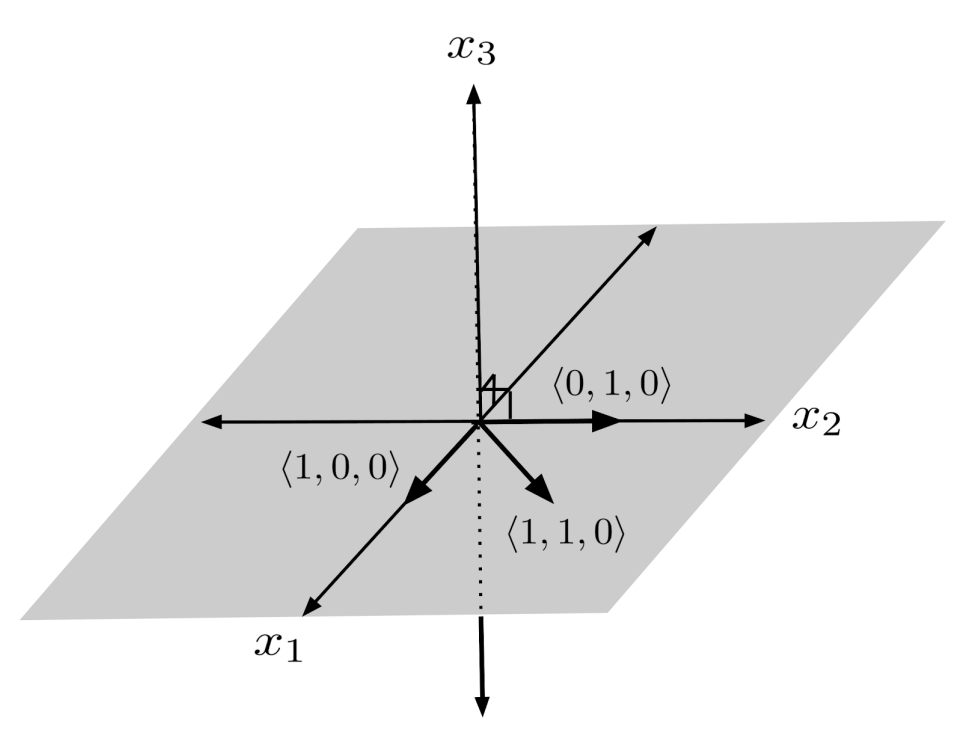
The vectors span the plane $x_3=0$. No matter how we combine vectors, the third component will always be $0$ – so we cannot reach any points above or below the plane, by adding multiples of vectors in the set.

Independence

In general, the dimension of the span of a set of vectors is equal to the number of independent vectors that remain after we remove the dependent vectors. A vector is said to be dependent if it can be written as a sum of multiples of other vectors in the set.

The labeling of vectors as independent or dependent depends on the order in which the vectors are considered, but regardless of order, removing all dependent vectors will leave the same number of independent vectors, even if the independent vectors themselves are different for different orders.

For example, in the set $\left\lbrace \left< 1,0,0 \right>, \left< 0,1,0 \right>, \left< 1,1,0 \right> \right\rbrace$ we can start by looking at the first vector, $\left< 1,0,0 \right>$. This vector is dependent since it can be produced by subtracting the other two vectors: $\left< 1,0,0 \right> = \left< 1,1,0 \right> - \left< 0,1,0 \right>$. Removing this vector from the set yields the reduced set $\left\lbrace \left< 0,1,0 \right>, \left< 1,1,0 \right> \right\rbrace$, which contains two independent vectors and thus cannot be reduced any further.

Since the fully reduced set has two independent vectors, it spans a 2-dimensional plane, and since the original set has the same span as the reduced set, the original set also spans the same 2-dimensional plane.

Alternatively, beginning with the original set $\left\lbrace \left< 1,0,0 \right>, \left< 0,1,0 \right>, \left< 1,1,0 \right> \right\rbrace$ we can start by looking at the second vector, $\left< 0,1,0 \right>$. This vector is dependent since it can be produced by subtracting the other two vectors: $\left< 0,1,0 \right> = \left< 1,1,0 \right> - \left< 1,0,0 \right>$. Removing this vector from the set yields the reduced set $\left\lbrace \left< 1,0,0 \right>, \left< 1,1,0 \right> \right\rbrace$, which contains two independent vectors and thus cannot be reduced any further.

Again, since the fully reduced set has two independent vectors, it spans a 2-dimensional plane, and since the original set has the same span as the reduced set, the original set also spans the same 2-dimensional plane.

The last alternative, beginning with the original set $\left\lbrace \left< 1,0,0 \right>, \left< 0,1,0 \right>, \left< 1,1,0 \right> \right\rbrace$, is to start by looking at the third vector, $\left< 1,1,0 \right>$. This vector is dependent since it can be produced by adding the other two vectors: $\left< 1,1,0 \right> = \left< 0,1,0 \right> + \left< 1,1,0 \right>$. Removing this vector from the set yields the reduced set $\left\lbrace \left< 1,0,0 \right>, \left< 0,1,0 \right> \right\rbrace$, which contains two independent vectors and thus cannot be reduced any further.

Again, since the fully reduced set has two independent vectors, it spans a 2-dimensional plane, and since the original set has the same span as the reduced set, the original set also spans the same 2-dimensional plane.

Maximum Number of Independent Vectors

Since the number of independent vectors in a set tells us the dimension of the span of that set, we can make the general conclusion that a set of N-dimensional vectors can have at most N independent vectors.

The N-dimensional vectors reside in N-dimensional space, so the largest space they can possibly span is their full N-dimensional space. Consequently, it’s not possible for the set of vectors to contain more than N independent vectors – otherwise, they would need to span a space of more than N dimensions.

For example, consider the following set of vectors:

Looking at the first two vectors $\left< 1,1 \right>$ and $\left< 1,-2 \right>$, we see that these two vectors are independent since they are not multiples of each other. As a result, the span of the vectors must have a dimension of at least 2.

But the vectors reside in 2-dimensional space, so their span is limited to at most 2 dimensions. Thus, we can conclude that the set of vectors spans exactly 2 dimensions, and that the third and fourth vectors in the set must be dependent, without even needing to check whether they can be written as sums of multiples of the first two vectors.

Now, consider the following set of vectors:

We can tell the first two vectors $\left< 1,-1,1,2 \right>$ and $\left< 2,0,4,2 \right>$ are independent since they aren’t multiples of each other, but it’s harder to see whether the remaining two vectors $\left< -1,3,3,2 \right>$ and $\left< 3,-4,1,4 \right>$ are independent because we also have to make sure they can’t be written as sums of multiples of other vectors in the set.

Reduction

To make it easier for us to tell whether these vectors are independent, we can reduce the set of vectors to a simpler set with the same span, by adding multiples of vectors from each other.

To begin the process of reduction, we can add multiples of the first vector to the other vectors so that we eliminate the first component from each of the other vectors.

• • The second vector has a first component of $2$, so we can eliminate it by adding $-2$ times the first vector.
• • The third vector has a first component of $-1$, so we can eliminate it by adding $1$ times the first vector.
• • The fourth vector has a first component of $3$, so we can eliminate it by adding $-3$ times the first vector.

The resulting set of vectors is shown below.

Since we only added multiples of vectors, we haven’t changed the span at all. But now all of the first components are zero EXCEPT for the first component in the first vector, so we can see that the first vector cannot be written as a sum of other vectors in the set. All the other vectors have zero in their first component, so every time we add multiples of them, the result will still have zero in the first component.

To check whether the second vector is independent, we can add multiples of the second vector to the remaining vectors to eliminate their second components.

But to make this easier, we can start by rescaling (i.e. multiplying) the second vector to have a second component of $1$. Its second component is currently $2$, so to convert $2$ to $1$, we need to multiply by $\frac{1}{2}$.

Now, we can add multiples of the second vector to the third and fourth vectors so that we eliminate their second components.

• • The third vector has a second component of $2$, so we can eliminate it by adding $-2$ times the second vector.
• • The fourth vector has a second component of $-1$, so we can eliminate it by adding $1$ times the second vector.

Clearly, the second vector cannot be written as a sum of multiples including the first vector, since including the first vector would cause the first component to become nonzero. And the second vector cannot be written as a sum of multiples of the third and fourth vectors, either, because no combination of them can produce a nonzero second component. So the second vector must be independent.

To determine whether the third and fourth vectors are independent, we can repeat the usual process once more. First, we’ll rescale the third vector by $\frac{1}{2}$ so that its first component is $1$.

The result is shown below.

The fourth vector has a third component of $-1$, so we can eliminate it by adding $1$ times the third vector.

Our final result is shown below.

We see that the first three vectors are independent, whereas the fourth vector is dependent since it is a multiple of every vector in the set (you can multiply any other vector by $0$ to obtain the fourth vector). As a result, our set spans a 3-dimensional subspace of 4-dimensional space.

Exercises

Tell the dimension of the span of the set of vectors. (You can view the solution by clicking on the problem.)

This post is part of the book Justin Math: Linear Algebra. Suggested citation: Skycak, J. (2019). Span, Subspaces, and Reduction. In Justin Math: Linear Algebra. https://justinmath.com/span-subspaces-and-reduction/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.