Spaced Repetition vs Spiraling

by Justin Skycak (@justinskycak) on March 02, 2024

By periodically revisiting content, a spiral curriculum periodically restores forgotten knowledge and leverages the spacing effect to slow the decay of that knowledge. Spaced repetition takes this line of thought to its fullest extent by fully optimizing the review process.

This post is part of the book The Math Academy Way (Working Draft, Jan 2024). Suggested citation: Skycak, J., advised by Roberts, J. (2024). Spaced Repetition vs Spiraling. In The Math Academy Way (Working Draft, Jan 2024). https://justinmath.com/spaced-repetition-vs-spiraling/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Some curricula adopt a spiral approach where material is naturally revisited and further built upon in later textbook chapters and/or grades. Spiraling is clearly an improvement over the default mode of instruction, which includes little to no systematic review – and it allows teachers to make use of the spacing effect to some extent while teaching manually at a group level without the assistance of technology. However, spiraling is still nowhere near the level of granularity, precision, and individualization that is required to capture the maximum benefit of true spaced repetition.

Note that while spiraling is sometimes conflated with discovery learning (both are widely attributed to psychologist Jerome Bruner in the 1960s), these are really two separate ideas, the latter of which I do not intend to endorse. There are plenty of spiral curricula (e.g., Saxon Math) that leverage direct instruction instead of discovery learning. The discussion here shall be concerned purely with the extent to which spiraling leverages the spacing effect, not the method by which instruction is delivered.

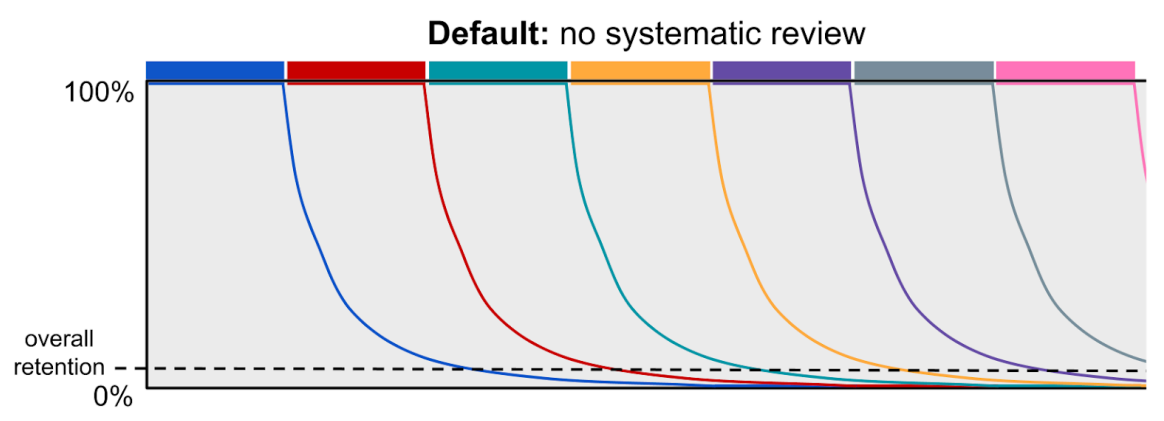
To understand the difference between spiraling and spaced repetition, it helps to visualize the corresponding forgetting curves. We start with the default mode of instruction, in which large groups of related material are covered all at once and are not systematically revisited in the future. Under this mode of instruction, students quickly forget what they learn, and their overall retention is extremely low.

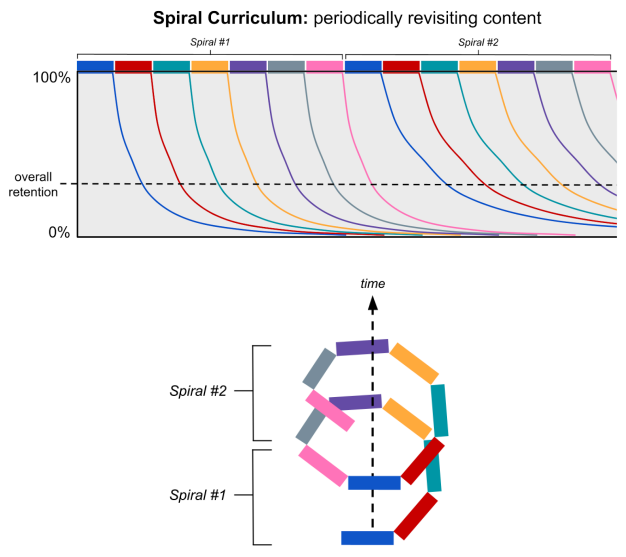
By periodically revisiting content, a spiral curriculum periodically restores forgotten knowledge and leverages the spacing effect to slow the decay of that knowledge. This raises students’ overall retention of what they have learned. To illustrate, a forgetting curve for a spiral curriculum with two spirals is shown below:

Spaced repetition takes this line of thought to its fullest extent by fully optimizing the review process. It precisely calibrates the spacing of reviews so as to maintain a consistently high level of retention and slow down the decay (i.e. stretch out the decay curves) as quickly as possible. Review spacing continually adapts to student performance, expanding in response to good performance and shrinking in response to poor performance. By optimizing the review process to the fullest extent, spaced repetition further raises students’ retention of what they have learned.

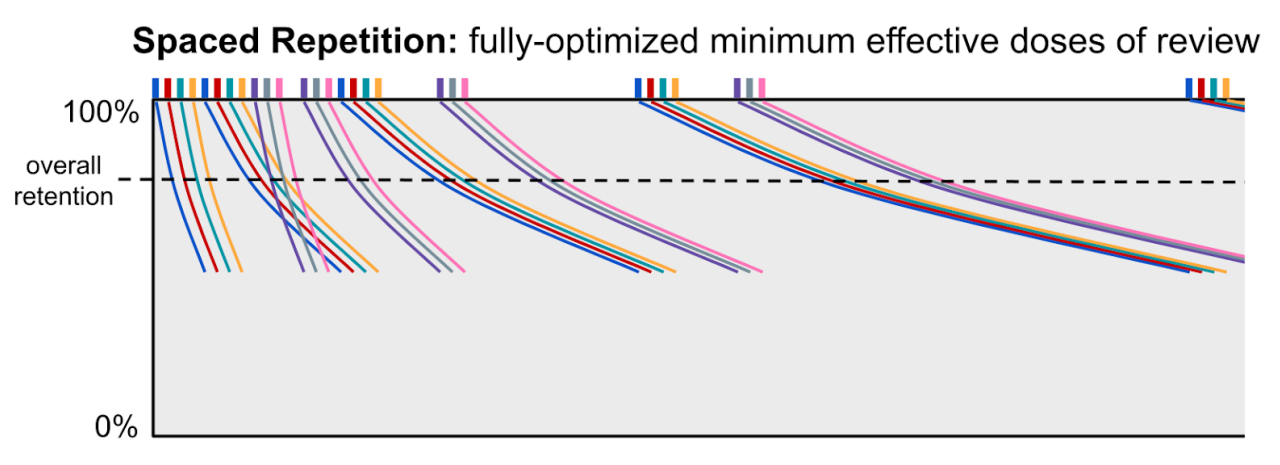
However, while spaced repetition is more optimal, it requires an inhuman amount of work from the instructor. Taken to its fullest extent, spaced repetition requires the instructor to keep track of a repetition schedule for every topic for every student and continually update that schedule based on the student’s performance – and each time a student learns (or reviews) an advanced topic, they’re implicitly reviewing many simpler topics, all of whose repetition schedules need to be adjusted as a result.

In this view, spiraling can be characterized as “the best an instructor can do” manually while teaching at a group level without the assistance of technology. Spaced repetition is the optimal solution to maximizing retention, but it is infeasible to perform spaced repetition manually, so spiraling is the next-best option that an instructor can actually perform without the assistance of technology.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.