Quadratic Systems

by Justin Skycak (@justinskycak) on

Systems of quadratic equations can be solved via substitution.

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Quadratic Systems. In Justin Math: Algebra. https://justinmath.com/quadratic-systems/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Systems of quadratic equations can be solved via substitution. After substituting, the resulting equation can itself be reduced down to a quadratic equation and solved by techniques covered in this chapter.

$\begin{align*} \text{Original system} \hspace{.5cm} &\Bigg| \hspace{.5cm} \begin{cases} y=2x^2-x \\ y=x^2-3x+3 \end{cases} \\ \text{Substitute for} y \hspace{.5cm} &\Bigg| \hspace{.5cm} 2x^2-x =x^2-3x+3 \\ \text{Convert to standard form} \hspace{.5cm} &\Bigg| \hspace{.5cm} x^2+2x-3=0 \\ \text{Solve for } x \hspace{.5cm} &\Bigg| \hspace{.5cm} x=-3 \text{ or } x=1 \\ \text{Evaluate } y \hspace{.5cm} &\Bigg| \hspace{.5cm} \begin{matrix} y=2(-3)^2-(-3)=21 \\ \text{or} \\ y=2(1)^2-2=1 \end{matrix} \\ \text{Solution} x \hspace{.5cm} &\Bigg| \hspace{.5cm} (-3,21) \text{ or } (1,1) \end{align*}$


Note that when evaluating $y$, it doesn’t matter which equation we use from the original equation. In the example above, we used the first equation because it was easier to compute, but using the second equation leads us to the same solutions.

$\begin{align*} &y=(-3)^2-3(-3)+3 = 21 \\ &\text{or} \\ &y=(1)^2-3(1)+3=1 \end{align*}$


Number of Solutions

There can be $2$, $1$, or $0$ points of intersection, depending on the arrangement of the parabolas.

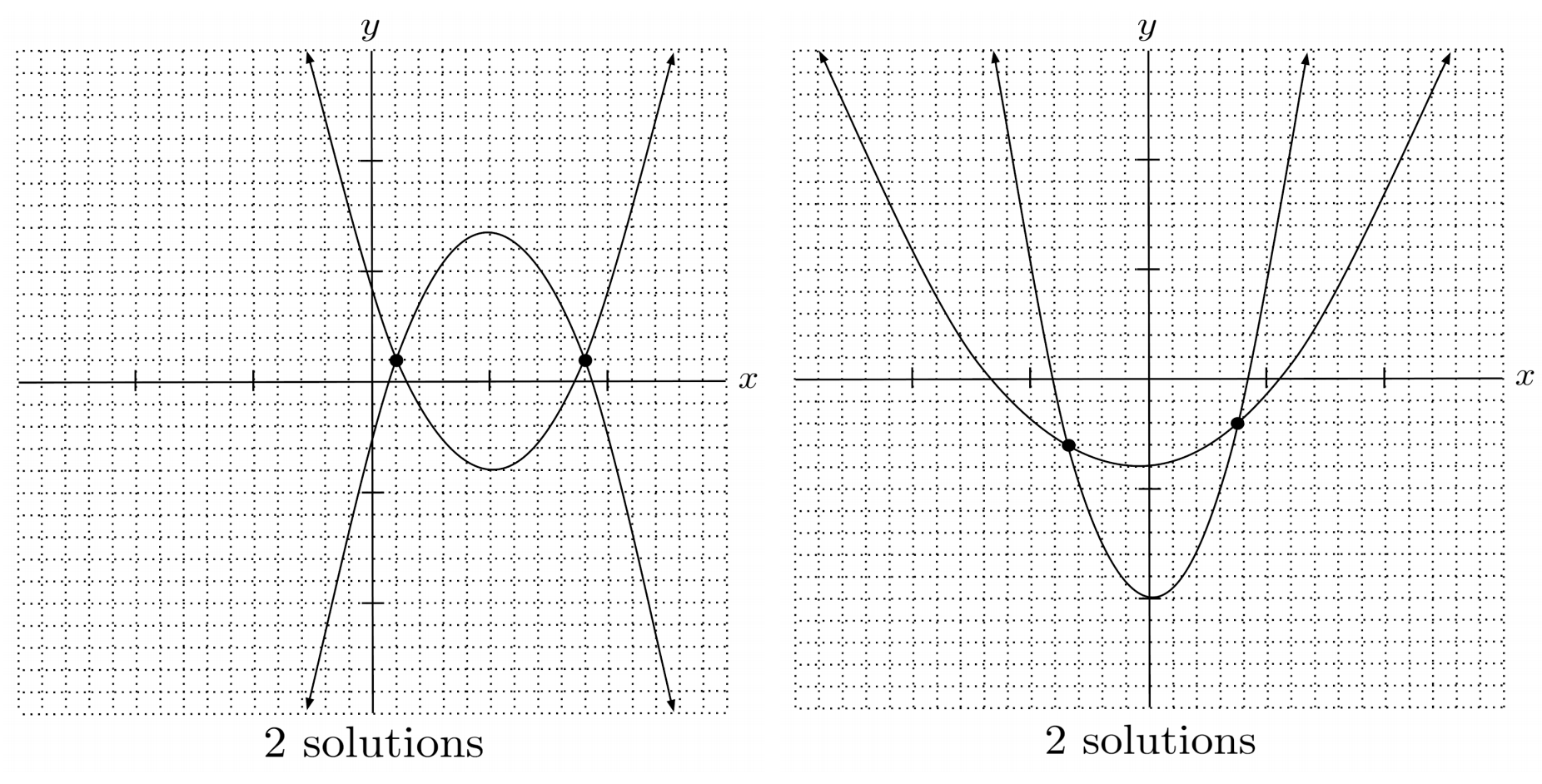
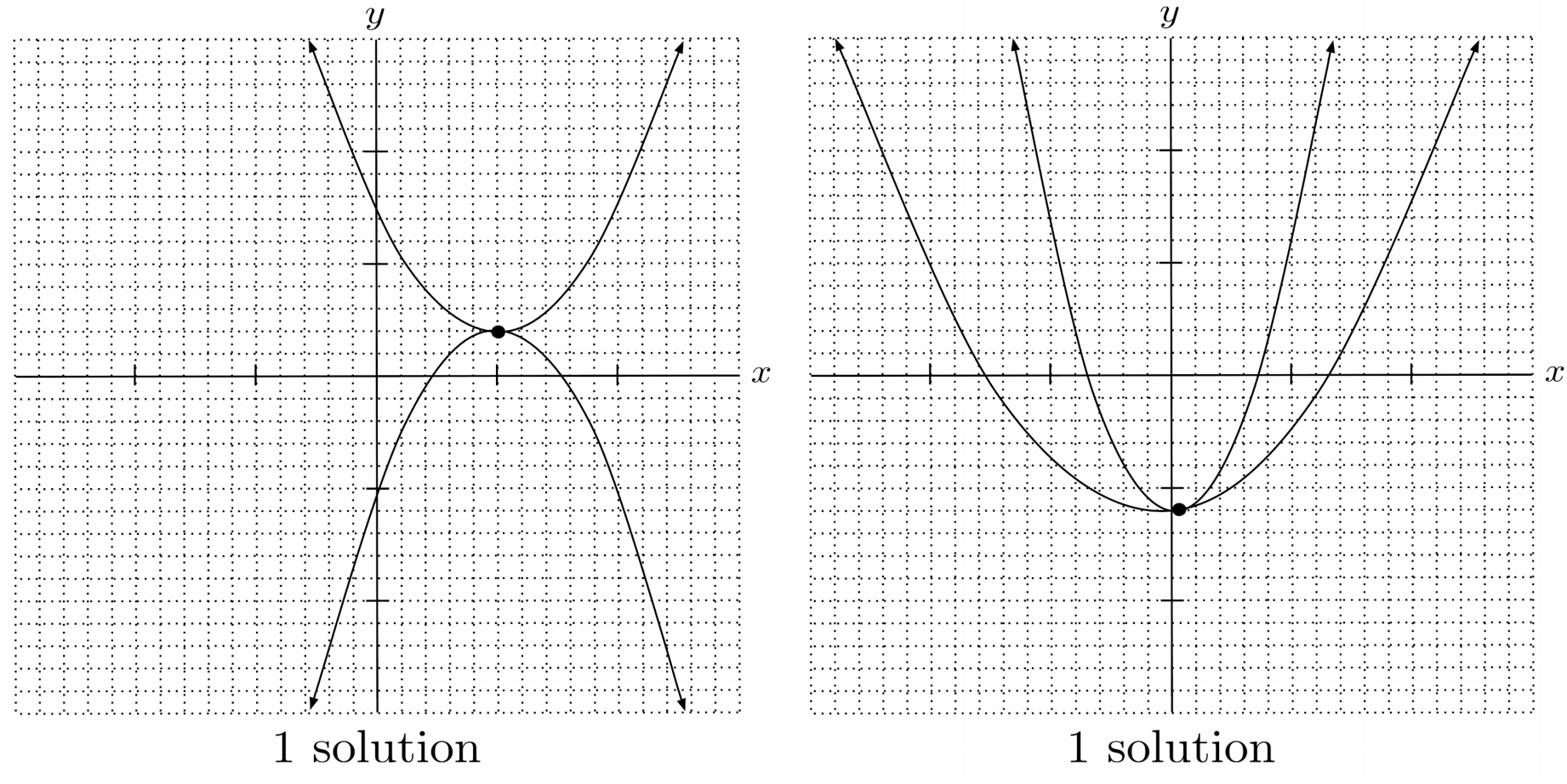
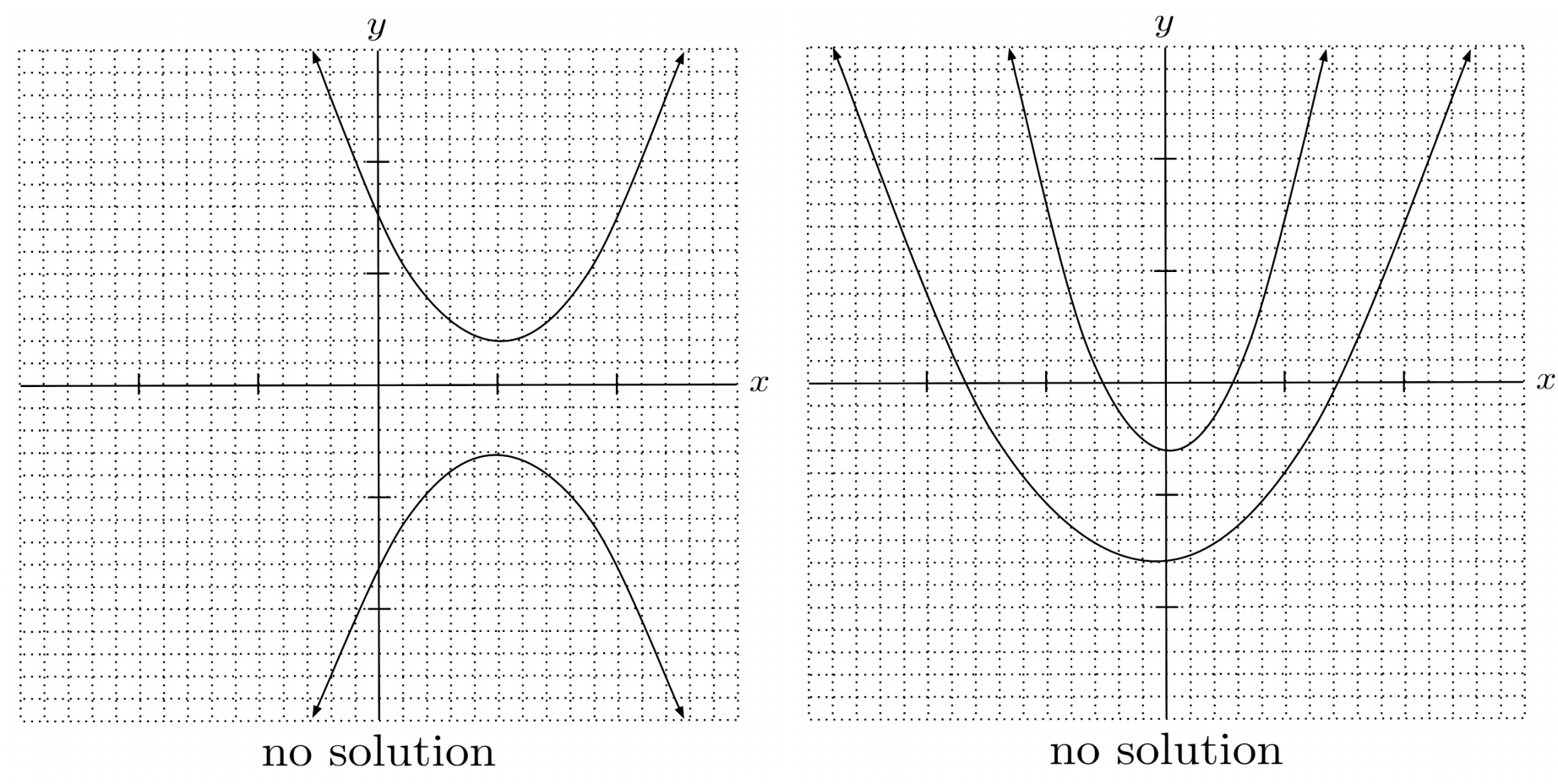
image


image


image


Just like in linear equations, if the result reduces down to a true statement, then there are infinitely many solutions because both equations in the system actually represent the same parabola.

$\begin{align*} \text{Original system} \hspace{.5cm} &\Bigg| \hspace{.5cm} \begin{cases} y=x^2+2x-3 \\ 2y=2x^2+4x-6 \end{cases} \\ \text{Substitute for} y \hspace{.5cm} &\Bigg| \hspace{.5cm} 2(x^2+2x-3)=2x^2+4x-6 \\ \text{Simplify} \hspace{.5cm} &\Bigg| \hspace{.5cm} 0=0 \\ \text{Solution} \hspace{.5cm} &\Bigg| \hspace{.5cm} \begin{matrix} \text{all points on} \\ y=x^2+2x-3 \end{matrix} \end{align*}$


On the other hand, if the result reduces down to a false statement, then there are no solutions because the parabolas never intersect.

$\begin{align*} \text{Original system} \hspace{.5cm} &\Bigg| \hspace{.5cm} \begin{cases} y=x^2+1 \\ y=x^2-1 \end{cases} \\ \text{Substitute for} y \hspace{.5cm} &\Bigg| \hspace{.5cm} x^2+1=x^2-1 \\ \text{Simplify} \hspace{.5cm} &\Bigg| \hspace{.5cm} 1=-1 \\ \text{Solution} x \hspace{.5cm} &\Bigg| \hspace{.5cm} \text{no solution} \end{align*}$


Exercises

Solve the following systems of quadratic equations. (You can view the solution by clicking on the problem.)

$1) \hspace{.5cm} \begin{cases} y=x^2+3x+6 \\ y=-x^2+13x-6 \end{cases}$
Solution:
$(2,16) \hspace{.5cm} (3,24)$


$2) \hspace{.5cm} \begin{cases} y=2x^2+6x+3 \\ y=2x^2+5x-2 \end{cases}$
Solution:
$(-5,23)$


$3) \hspace{.5cm} \begin{cases} y=3x^2+7x+9 \\ y=2x^2+7x+10 \end{cases}$
Solution:
$(1,19) \hspace{.5cm} (-1,5)$


$4) \hspace{.5cm} \begin{cases} y=x^2+3x+2 \\ y=-2x^2+x-5 \end{cases}$
Solution:
$\text{no solution}$


$5) \hspace{.5cm} \begin{cases} y=x^2+8x-2 \\ y=x^2+5x \end{cases}$
Solution:
$\left( \frac{2}{3}, \frac{34}{9} \right)$


$6) \hspace{.5cm} \begin{cases} y=-x^2-7x-10 \\ y=-2x^2-14x-20 \end{cases}$
Solution:
$(-2,0) \hspace{.5cm} (-5,0)$


$7) \hspace{.5cm} \begin{cases} y=5x^2-x+7 \\ y=x^2+2x+1 \end{cases}$
Solution:
$\text{no solution}$


$8) \hspace{.5cm} \begin{cases} y=x^2-10x+10 \\ y=-x^2+x-5 \end{cases}$
Solution:
$\left( \frac{5}{2}, -\frac{35}{4} \right) \hspace{.5cm} (3,-11)$

This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Quadratic Systems. In Justin Math: Algebra. https://justinmath.com/quadratic-systems/


Want to get notified about new posts? Join the mailing list and follow on X/Twitter.