Quadratic Inequalities
Quadratic inequalities are best visualized in the plane.
This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Quadratic Inequalities. In Justin Math: Algebra. https://justinmath.com/quadratic-inequalities/
Want to get notified about new posts? Join the mailing list and follow on X/Twitter.
Quadratic inequalities are best visualized in the plane. For example, to solve a quadratic inequality $-x^2+x+2>0$, we can find the values of $x$ where the parabola $y=-x^2+x+2$ is positive.
Since $y=-x^2+x+2$ is a downward parabola, the solution consists of the values of $x$ in its midsection which arches over the x-axis. That is, the solution consists of all x-values between the solutions to $-x^2+x+2=0$.
This quadratic equation factors to $-(x-2)(x+1)=0$, so the parabola’s midsection is given by $-1<x<2$, or $(-1,2)$ in interval notation.
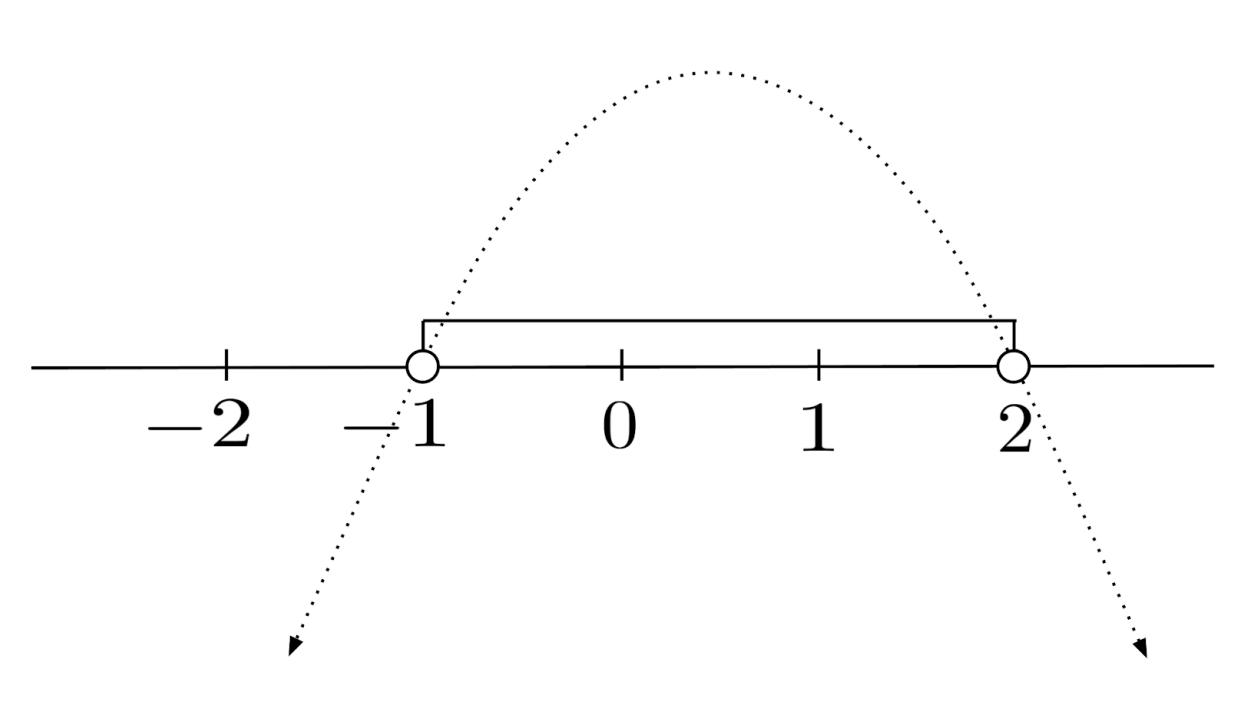
Case when the Solution is a Union
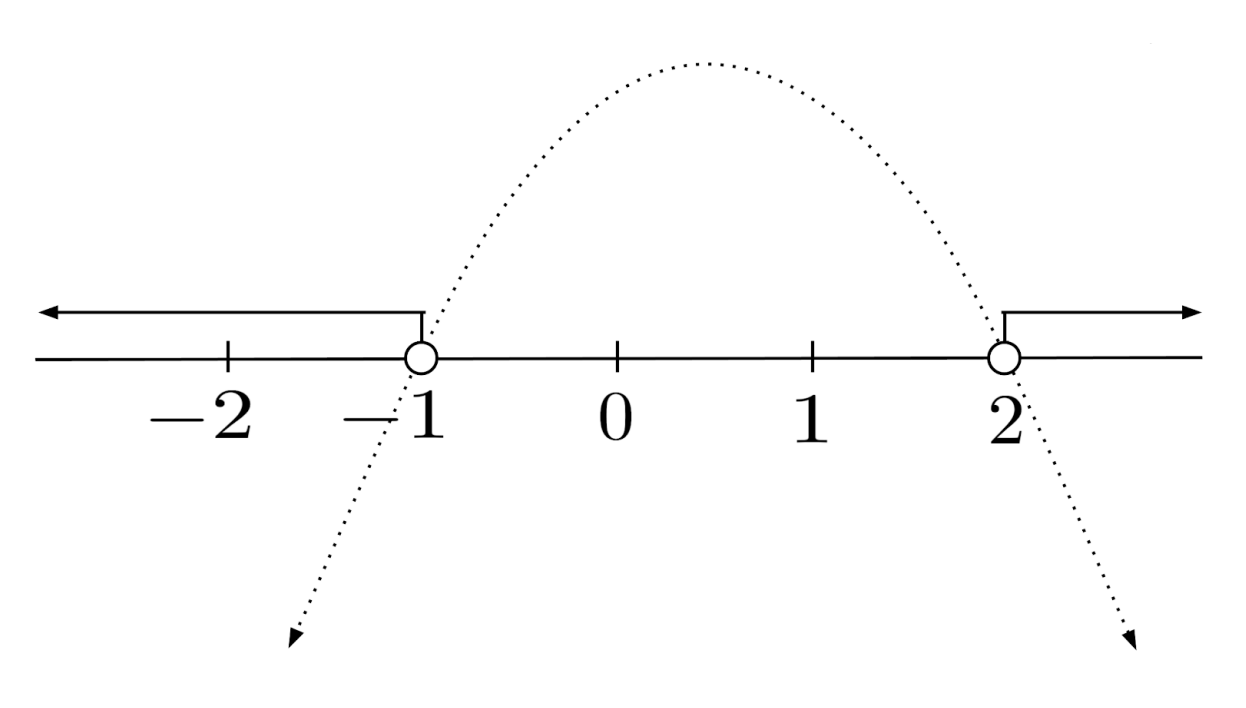
On the other hand, if we want to solve $-x^2+x+2<0$, then we need to find the values of $x$ where the parabola $y=-x^2+x+2$ is negative.
This time, the solution consists of all the values of $x$ in the arms of the parabola which extend under the x-axis. That is, the solution consists of all x-values less than the leftmost solution or greater than the rightmost solution to $-x^2+x+2=0$.
The solution of the inequality is then given by $x<-1 \text{ or } x>2$, which is $(-\infty, -1) \cup (2, \infty)$ in interval notation. (The $\cup$ symbol is called a union, and it allows us to include multiple segments in interval notation.)
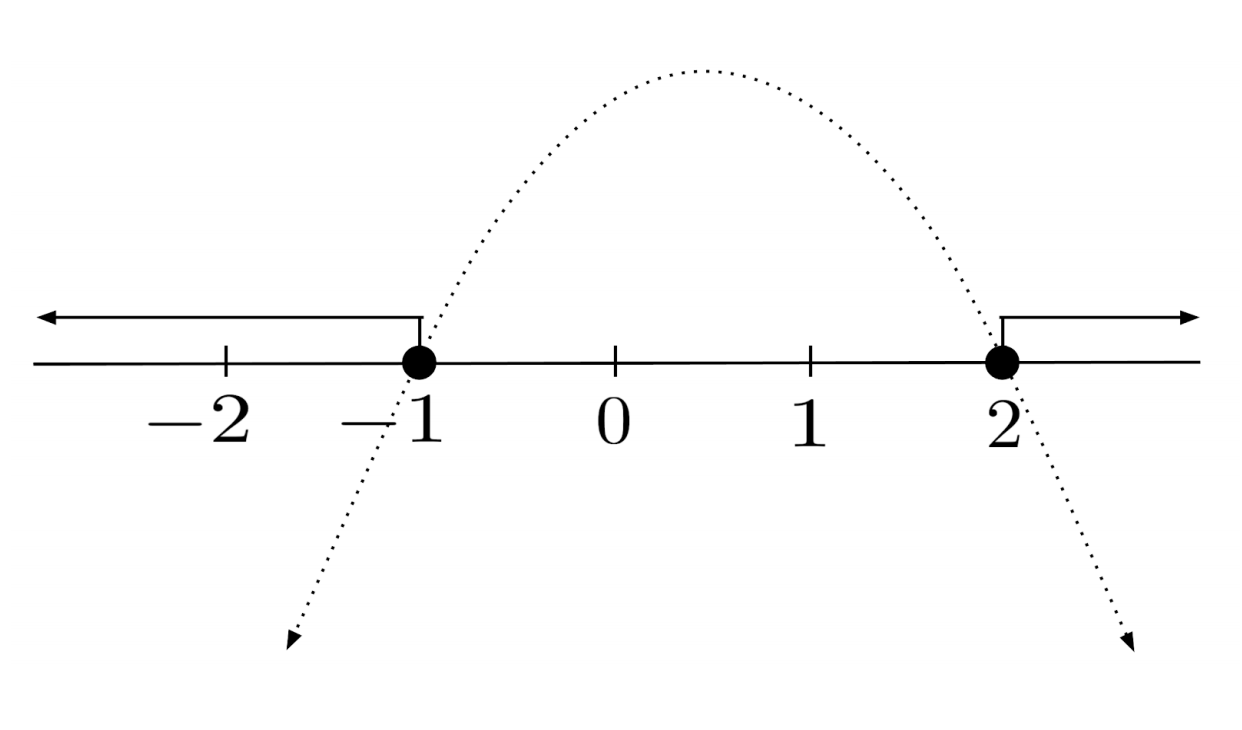
To solve $-x^2+x+2 \leq 0$, we just need to propagate the allowance of equality to our final answer. Thus, the solution is $x \leq -1 \text{ or } x \geq 2$, which is $(-\infty, -1] \cup [2,\infty)$ in interval notation.
Case when the Parabola is Never Zero
When a quadratic inequality involves a parabola that is never zero, there is either no solution or the solution is all real numbers.
For example, the parabola $y=x^2+5$ has only positive y-values, so $x^2+5<0$ has no solution and $x^2+5>0$ is solved by all real numbers.
In interval notation, we express all real numbers as the full number line $(-\infty, \infty)$, and we express no solution as $\emptyset$. (The $\emptyset$ symbol is called the empty set, and it represents an interval which doesn’t contain any numbers.)
Exercises
Solve the following inequalities, writing the solutions in interval notation. (You can view the solution by clicking on the problem.)
$1) \hspace{.5cm} x^2-4 \geq 0$
Solution:
$(-\infty,-2] \cup [2,\infty)$
$2) \hspace{.5cm} x^2+1 > 0$
Solution:
$(-\infty,\infty)$
$3) \hspace{.5cm} -3x^2+27<0$
Solution:
$(-\infty,-3) \cup (3,\infty)$
$4) \hspace{.5cm} x^2-9x+14<0$
Solution:
$(2,7)$
$5) \hspace{.5cm} x^2+x+1 \leq 0$
Solution:
$\emptyset$
$6) \hspace{.5cm} 2x^2 \geq 7x+15$
Solution:
$\left( -\infty, -\frac{3}{2} \right] \cup \left[ 5,\infty \right)$
$7) \hspace{.5cm} x+1 < 6x^2$
Solution:
$\left( -\infty, -\frac{1}{3} \right) \cup \left( \frac{1}{2}, \infty \right)$
$8) \hspace{.5cm} -x^2-7x+30 > x^2+7x-30$
Solution:
$(-10,3)$
$9) \hspace{.5cm} 10x(x-3) \leq 7+3x$
Solution:
$\left[ -\frac{1}{5}, \frac{7}{2} \right]$
$10) \hspace{.5cm} (3x+5)^2 \geq 3(x^2-1)+7(x-11)$
Solution:
$\left( -\infty, \infty \right)$
This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Quadratic Inequalities. In Justin Math: Algebra. https://justinmath.com/quadratic-inequalities/
Want to get notified about new posts? Join the mailing list and follow on X/Twitter.