One of the Weirdest, Most Treacherous Math Problems You Will Ever Encounter

by Justin Skycak (@justinskycak) on

A limit problem conjured up from the depths of hell.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Anyone who’s taken calculus: can you solve this math problem?

It might look simple but it’s actually one of the weirdest, most treacherous problems you’ll ever encounter.

Go ahead, give it a try before reading on.

$\begin{align*} \lim\limits_{(x,y) \to 0} \frac{x^2y}{x^4+y^2} \end{align*}$
image

(a comment on my StackExchange answer introducing this problem)

The result is NOT correct if you pretend the limit only has one variable.

$\begin{align*} \lim\limits_{x \to 0} \frac{x^2x}{x^4+x^2} = \lim\limits_{x \to 0} \frac{x}{x^2+1} = \frac{0}{1} = 0 \end{align*}$


Doing so evaluates the limit along the path $y=x,$ just one of many possible paths by which we could approach the point $(0,0).$

Now, if you’ve taken multivariable calc, you probably knew that already.

But did you know that if you evaluate the limit along ALL lines through the origin, you STILL get a result of 0, and that result of 0 is still INCORRECT!

$\begin{align*} {\small \left. \begin{matrix} \textrm{along} \\[-3pt] y=mx \\[-3pt] m\neq 0\end{matrix} \phantom{i} \right\vert} & \phantom{x} \lim\limits_{x \to 0} \frac{x^2(mx)}{x^4+(mx)^2} = \lim\limits_{x \to 0} \frac{mx}{x^2+m^2} = \frac{0}{m^2} = 0 \\ {\small \left. \begin{matrix} \textrm{along} \\[-3pt] y=0\end{matrix} \phantom{i} \right\vert} & \phantom{x} \lim\limits_{x \to 0} \frac{x^2(0)}{x^4+0^2} = 0 \\ {\small \left. \begin{matrix} \textrm{along} \\[-3pt] x=0\end{matrix} \phantom{i} \right\vert} & \phantom{x} \lim\limits_{y \to 0} \frac{(0^2)y}{0^4+y^2} = 0 \end{align*}$


Why is this still incorrect? Because we’ve only checked LINEAR paths. You get a different result if you check the NON-linear path $y=x^2.$

Our limit evaluates to 0 along all LINEAR paths, but NOT along all paths IN GENERAL.

It comes out to $\frac{1}{2}$ along the quadratic path $y=x^2.$

$\begin{align*} \lim\limits_{x \to 0} \frac{x^2(x^2)}{x^4+(x^2)^2} = \lim\limits_{x \to 0} \frac{x^4}{x^4+x^4} = \frac{x^2}{2x^4} = \dfrac{1}{2} \end{align*}$


So, generally speaking, the answer is that THE LIMIT DOES NOT EXIST.

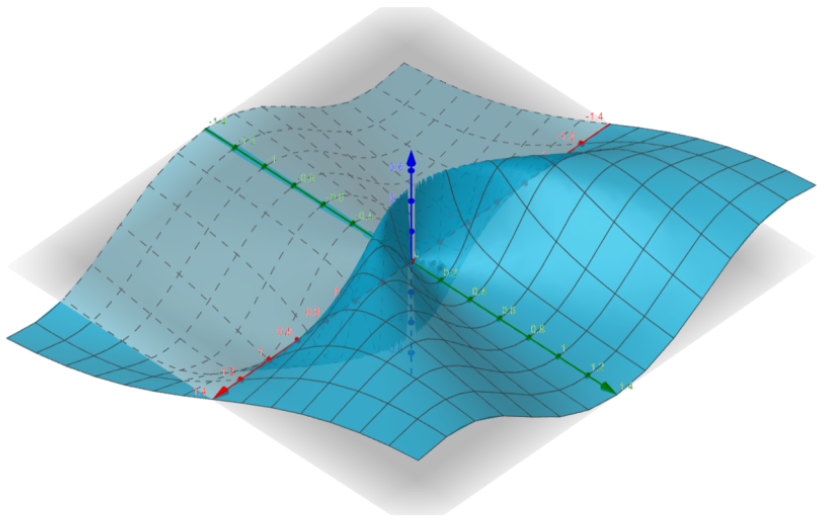
To better understand this, you can take a look at the graph.

It’s super weird and counterintuitive that you can approach the SAME place through all linear paths, yet approach a DIFFERENT place through a quadratic path.

But it’s true, and the graph below shows how it’s possible:

image



Want to get notified about new posts? Join the mailing list and follow on X/Twitter.