Minimax Strategy

by Justin Skycak (@justinskycak) on March 02, 2022

Repeatedly choosing the action with the best worst-case scenario.

This post is part of the book Introduction to Algorithms and Machine Learning: from Sorting to Strategic Agents. Suggested citation: Skycak, J. (2022). Minimax Strategy. In Introduction to Algorithms and Machine Learning: from Sorting to Strategic Agents. https://justinmath.com/minimax-strategy/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

The minimax strategy is a powerful game-playing strategy that operates on game trees. It envisions the worst-case scenario that could possibly result from any given move, and then chooses the move that would result in the best (i.e. “least bad”) worst-case scenario.

Minimax Algorithm

The minimax strategy chooses actions according to the following algorithm:

Create a game tree with all the states of the game.
Identify each node that represents a terminal state and assign it a minimax value of $1,$ $-1,$ or $0$ depending on whether it corresponds to a win, loss, or tie for you.
Repeatedly propagate those values up the tree to parent nodes, assuming that you will try to win (i.e. move into states that maximize your value) and your opponent will try to make you lose (i.e. move into states that minimize your value).

If the edge from the parent node corresponds to your turn, then the parent node's minimax value is the maximum of the child values (because you want to maximize your value).
Otherwise, if the edge from the parent node corresponds to your opponent's turn, then the parent node's minimax value is the minimum of the child values (because your opponent wants to minimize your value).

Always choose the move that takes you to the next possible state with the highest minimax value. (You can break ties via random choice.)

Worked Example

To illustrate the minimax algorithm in action, let’s label part of a tic-tac-toe game tree with minimax values, from the perspective of player X (i.e. supposing we are player X). We always start by labeling the terminal states.

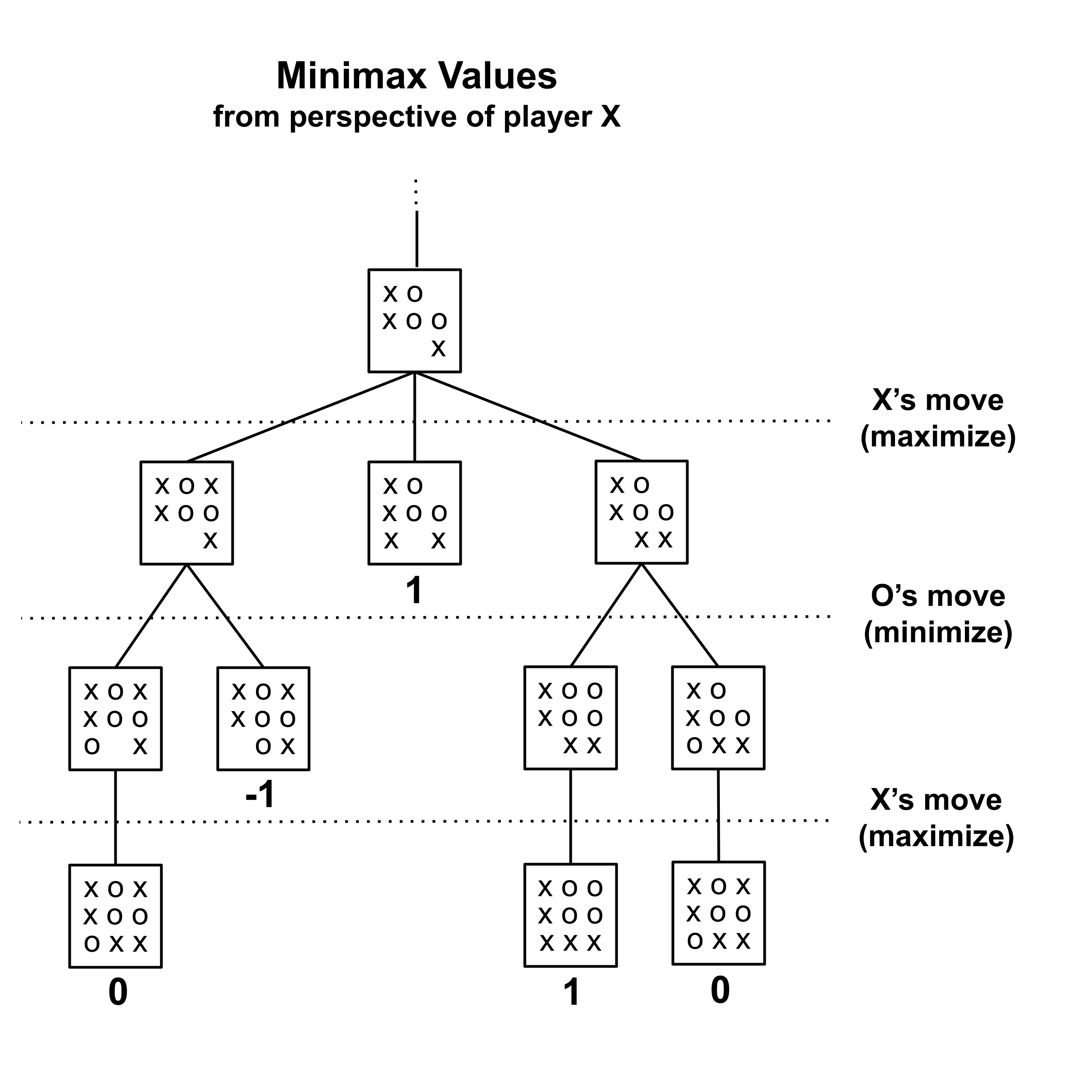
Then, we propagate these values up to parent nodes. But we can only compute the minimax value of a node once we’ve assigned minimax values to all its children.

Here, there are $3$ parents who do not have minimax values but whose children all do. The edges between these parents and their children all correspond to moves by X, which is us, and we want to maximize the minimax value. So, to each of these parents, we assign the maximum value of its children. (In this case, each of these parents has only one child, so the maximum value happens to be the only value.)

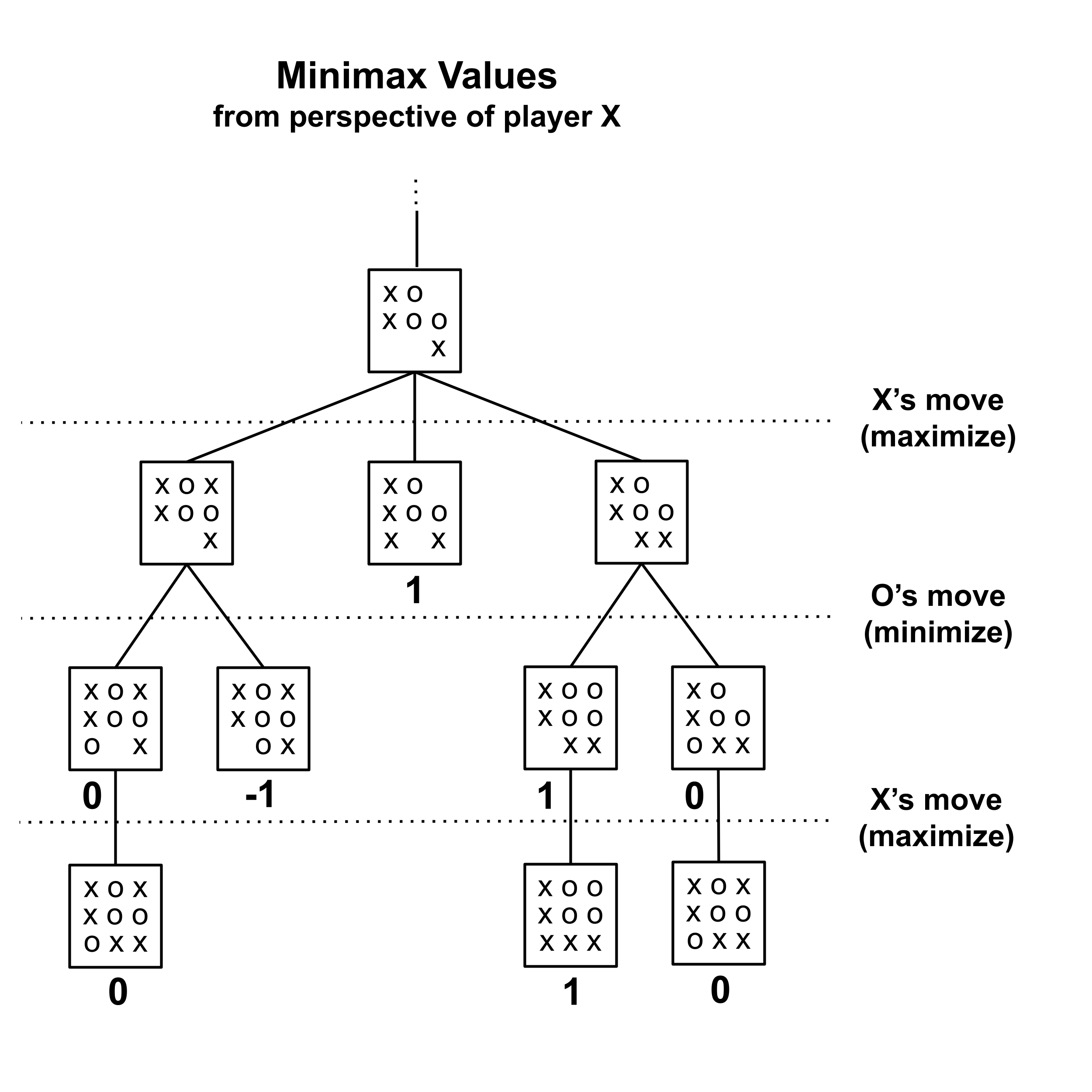
Now, we repeat the process. Now, there are $2$ parents who do not have minimax values but whose children all do. The edges between these parents and their children all correspond to moves by O, which is our opponent, and our opponent wants to minimize the minimax value. So, to each of these parents, we assign the minimum value of its children.

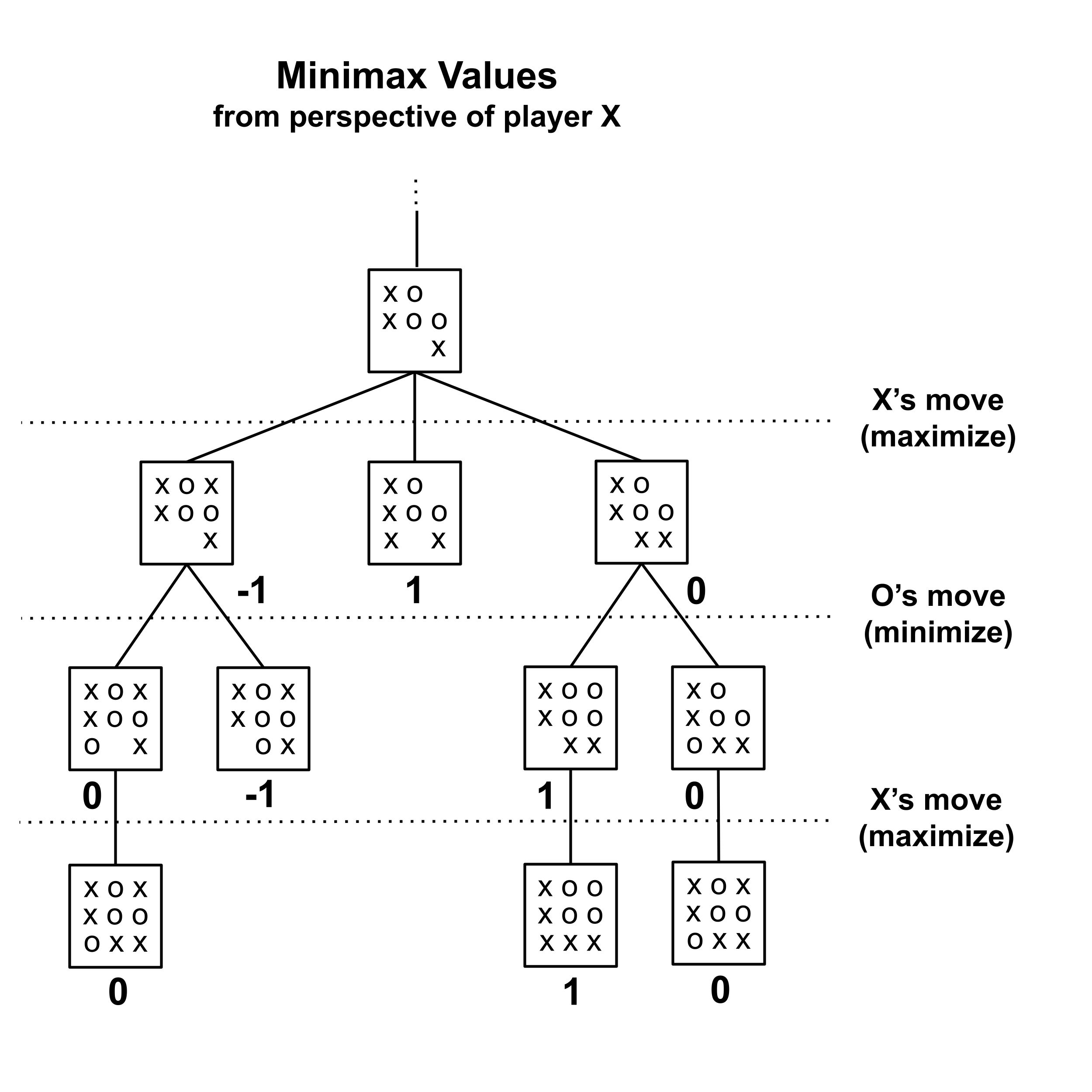
Again, we repeat the process. There is a single parent (the top node) who does not have a minimax value but whose children all do. The edges between these parents and their children all correspond to moves by X, which is us, and we want to maximize the minimax value. So we assign it the maximum value of its children.

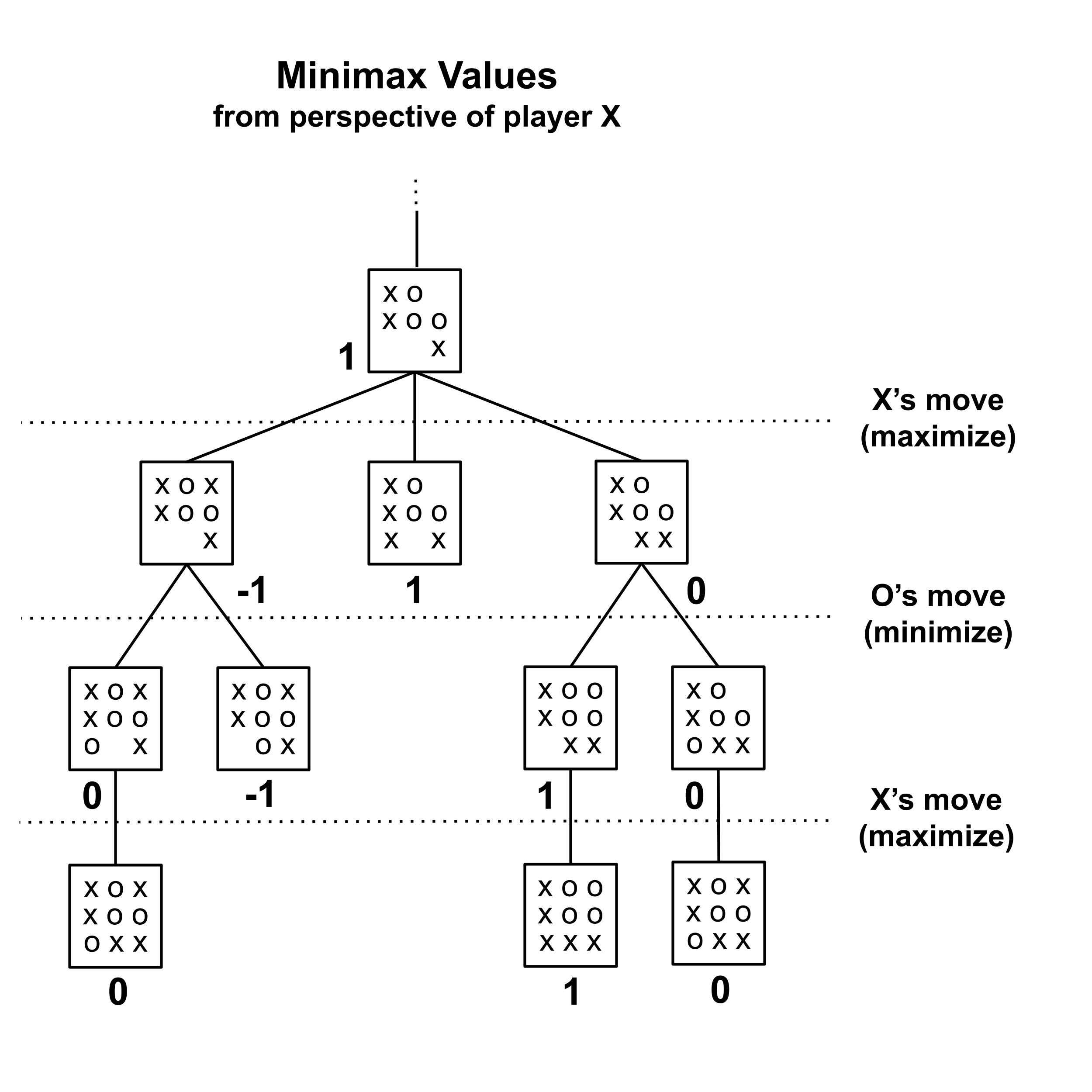
We’ve assigned minimax values to all the nodes in this part of the tree. The minimax value of the highest node is $1,$ which tells us that there is a guaranteed way to win from that game state (all we need to do is place an X in the bottom-left corner). Indeed, this action is accomplished by choosing the child node with the maximum value.

Exercises

Implement a minimax player for your tic-tac-toe game that automatically chooses actions based on the minimax strategy. (It goes without saying: don't rebuild and relabel the game tree on every move. That would be very inefficient and slow. Build and label it once at the beginning, and then use the same tree throughout the rest of the game.)
Run your minimax player against a deterministic "top-left strategy" that always moves into the leftmost open space in the topmost row. At each of the minimax player's turns, print out the possible moves that the minimax player could possibly make as well as the associated minimax values of the states. Check the following:

Every minimax value should be either $1,$ $-1,$ or $0.$
Each of the minimax player's chosen moves should be associated with a maximum-value state.
Towards the end of the game, you should be able to inspect game states, manually sketch out the section of the game tree containing their progeny, and then manually compute and verify the minimax value of each state.
Make sure these checks still hold when the minimax player goes second.

Then, run your minimax player against a random player for many games (alternating who goes first). The minimax player should never lose. If you encounter any game where the minimax player loses, then you'll need to store the sequence of moves and step through the game to debug what went wrong.
Play two minimax players against each other for many games, alternating who goes first. Every game should result in a tie.
Play against the minimax player yourself. You shouldn't be able to win.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.