Lines and Planes

A line starts at an initial point and proceeds straight in a constant direction. A plane is a flat sheet that makes a right angle with some particular vector.

This post is part of the book Justin Math: Linear Algebra. Suggested citation: Skycak, J. (2019). Lines and Planes. In Justin Math: Linear Algebra. https://justinmath.com/lines-and-planes/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

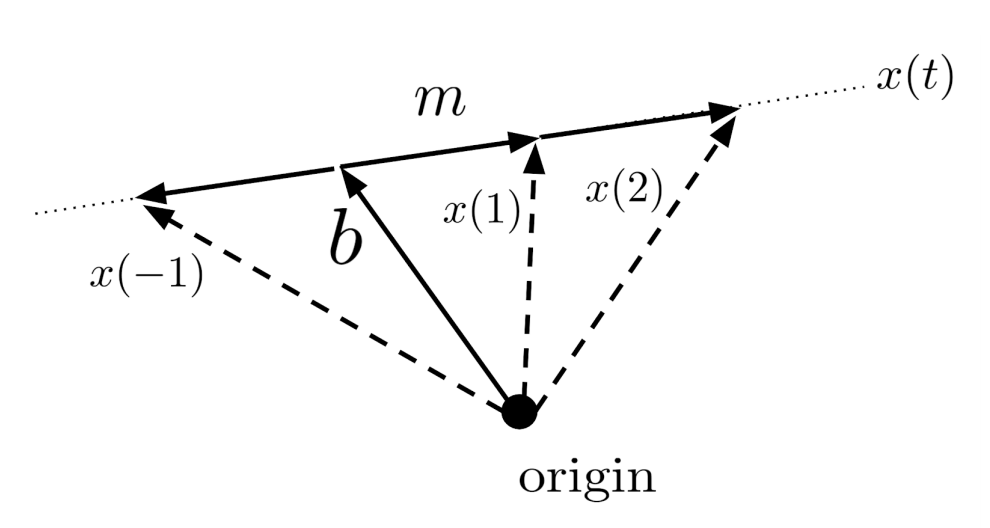
A line starts at an initial point and proceeds straight in a constant direction. Thus, we can write the equation of a line as

where

• • $b = \left< b_1, b_2, \ldots, b_N \right>$ is the initial point,
• • $m = \left< m_1, m_2, \ldots, m_N \right>$ is the constant direction in which the line travels, and
• • $x(t) = \left< x_1(t), x_2(t), \ldots, x_N(t) \right>$ is the point reached by traveling $t$ units away from $b$ in the direction of $m$.

(Though $x(t)$ is actually a vector, we can also refer to it as the point where the vector lands when the vector is placed at the origin.)

Finding the Equation of a Line

For example, to compute the line between the points $(1,2,3,4)$ and $(5,-2,3,7)$ in 4-dimensional space, we can start by computing the direction $m$ as the difference between the two points:

Taking $b=\left< 1,2,3,4 \right>$ as our initial point, then, we can express the line as

If we wanted to find another point on the line, we could substitute another value for $t$, say, $t=-2$.

Checking Whether a Point is on a Line

If we wanted to check whether the point $\left< -1,-2,-3,-4 \right>$ is on the line, we could substitute this point for $x(t)$ and try to solve for $t$.

Setting first components equal, we find $-2=4t$, which implies that $t=-\frac{1}{2}$. But equating second components yields $-4=-4t$, which implies that $t=1$. So, there is no solution that matches all pairs of components, and consequently the point $\left< -1,-2,-3,-4 \right>$ is not on the line.

However, we can verify that the point $\left< 9,-6,3,10 \right>$ is on the line using the same method.

Equating first components yields $8=4t$ which is valid for $t=2$; equating second components yields $-8=-4t$ which is also valid for $t=2$; equating third components yields $0=0$ which is valid for all choices of $t$; and equating fourth components yields $6=3t$ which is also valid for $t=2$. Thus the point $\left< 9,-6,3,10 \right>$ is on the line because it is simply $x(t)$ evaluated at $t=2$.

The Equation of a Plane

Now, let’s talk about how to write the equation of a plane in N-dimensional space. A plane can be visualized as a flat sheet that makes a right angle with some particular vector. Thus, a plane just consists of all vectors through some point in the plane, that are perpendicular to a single vector.

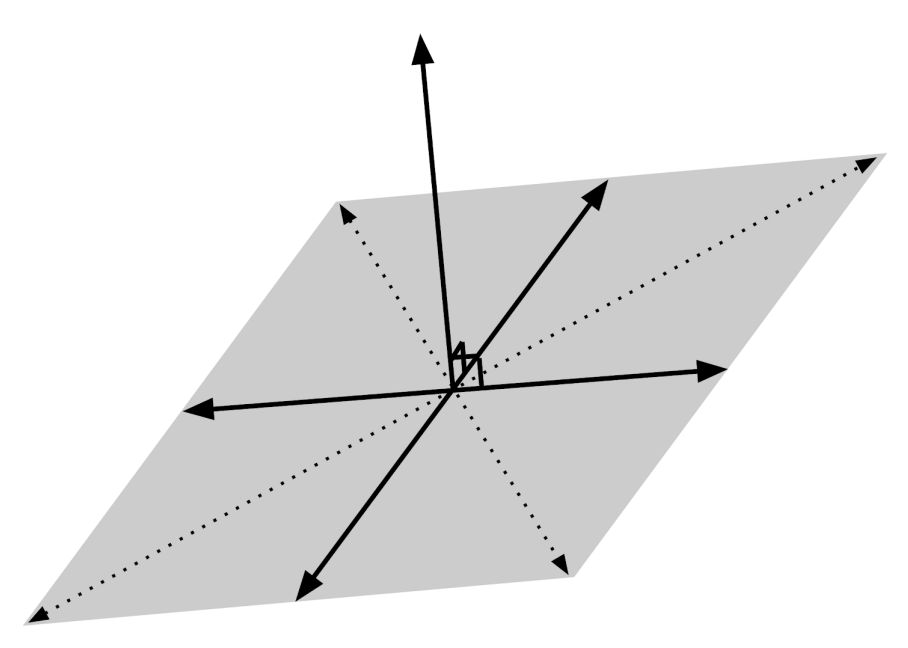
If $x_0$ is a point in the plane, then the vectors in the plane can be written $x-x_0$, where $x$ represents other points on the plane. These vectors are all perpendicular to a single vector, call it $a$, so their dot product must be zero: $a \cdot (x-x_0) = 0$.

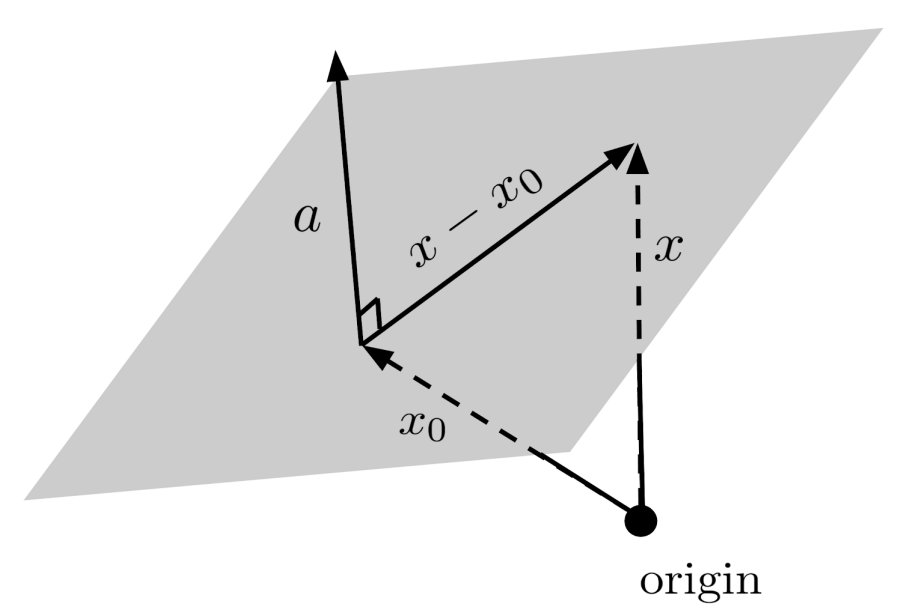
Distributing the dot product, we have $a \cdot x - a \cdot x_0 = 0$, and rearranging we have $a \cdot x = a \cdot x_0$. The right-hand side $a \cdot x_0$ is just a constant, so we can simply call it $k$. Thus, we have the general equation for a plane:

Here, $a$ is a vector that is perpendicular to the plane,$x$ are points on the plane, and $k$ is some constant. Writing $a=\left< a_1, a_2, \ldots, a_N \right>$ and $x = \left< x_1, x_2, \ldots, x_N \right>$, we can expand out the general equation for a plane into an equation consisting only of scalars:

Finding a Plane Given a Point and Perpendicular Vector

For example, to compute the plane that passes through the point $\left< 5,3,1 \right>$ and has a perpendicular vector of $\left< 1,-1,2 \right>$, we can start by setting up the equation with the perpendicular vector substituted.

To solve for $k$, we can simply substitute the point $\left< 5,3,1 \right>$ for $x$ and take the dot product.

Then, we can substitute for $k$ and expand out the dot product in the initial equation.

Now, suppose we have an equation for a plane, and we want to find the perpendicular vector.

To do this, we can simply organize the equation and convert it to the vector equation of the plane, using the dot product.

The perpendicular vector is just the first vector in the dot product, $\left< 2,-5,1,-1 \right>$.

Finding a Plane Given Three Points

Lastly, suppose that we want to find the equation of the plane that contains the three points $(1,2,3)$, $(5,4,-1)$, and $(-2,3,0)$.

To start off, we can find two vectors within the plane by starting at one of the points, say $(1,2,3)$, and computing the displacement vectors to the other two points:

These displacement vectors are within the plane, so if we can find a vector that is perpendicular to these displacement vectors, then we will have a vector that is normal to the plane.

Since these displacement vectors are 3-dimensional, we can compute their cross product, which yields a perpendicular vector.

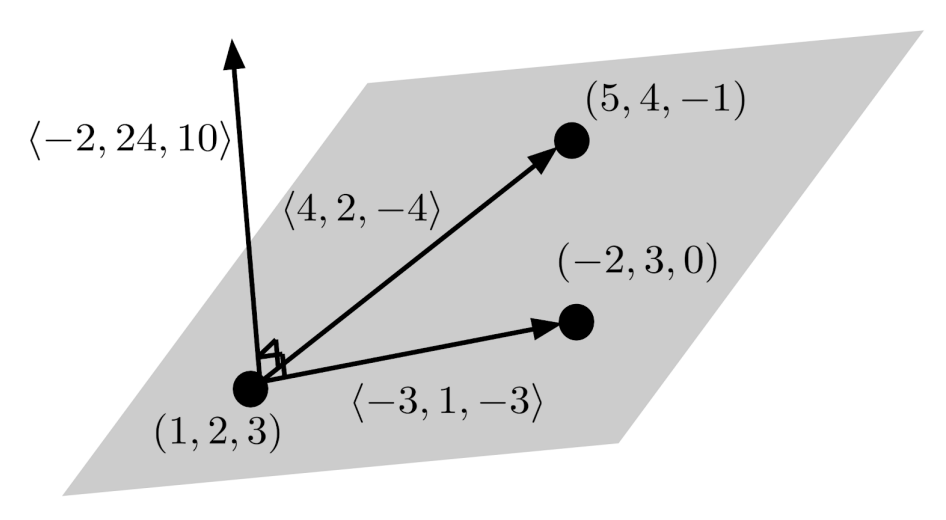
Using this vector as the normal vector of the plane, the equation of the plane becomes

for some constant $k$. To find the value of $k$, we can simply substitute one of the points in the plane, say, $(1,2,3)$.

Thus, the equation of the plane is

which can be simplified to

Looking back, we could have saved some work by using the vector $\left< 2,1,-2 \right>$ instead of the displacement vector $\left< 4,2,-4 \right>$, since $\left< 2,1,-2 \right>$ follows the same direction (it’s just half as long).

The normal vector resulting from the cross product would then have been $\left< -1,12,5 \right>$, which is the normal vector in the fully simplified equation of the plane.

(The vector $\left< -1,12,5 \right>$ points in the same direction as the original normal vector $\left< -2,24,10 \right>$; it’s just half as long.)

Exercises

Compute the equation of the line that passes through the given points. (You can view the solution by clicking on the problem.)

Check whether the given point $P$ is on the given line. If so, determine the value of $t$ for which $x(t)=P$. (You can view the solution by clicking on the problem.)

Write the equation of the plane that contains the given point $P$ and is perpendicular to the given normal vector $n$. (You can view the solution by clicking on the problem.)

Write the equation of the plane that contains the three given points. (You can view the solution by clicking on the problem.)

This post is part of the book Justin Math: Linear Algebra. Suggested citation: Skycak, J. (2019). Lines and Planes. In Justin Math: Linear Algebra. https://justinmath.com/lines-and-planes/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.