Layering: Building Structural Integrity in Knowledge

by Justin Skycak (@justinskycak) on February 17, 2024

Layering is the act of continually building on top of existing knowledge -- that is, continually acquiring new knowledge that exercises prerequisite or component knowledge. This causes existing knowledge to become more ingrained, organized, and deeply understood, thereby increasing the structural integrity of a student's knowledge base and making it easier to assimilate new knowledge.

This post is part of the book The Math Academy Way (Working Draft, Jan 2024). Suggested citation: Skycak, J., advised by Roberts, J. (2024). Layering: Building Structural Integrity in Knowledge. In The Math Academy Way (Working Draft, Jan 2024). https://justinmath.com/layering-building-structural-integrity-in-knowledge/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

As students learn progressively more advanced material, they reinforce and deepen their foundational knowledge. In academic literature, this is known as facilitation: when a new task exercises knowledge learned in a prior task, learning can be facilitated in two ways:

(Retroactive Facilitation) The new task can restore memory of prior knowledge to the same extent as identical repetition of the prior task, leading to long-lasting retention (Ausubel, Robbins, & Blake, 1957; Arzi, Ben-Zvi, & Ganiel, 1985).
(Proactive Facilitation) Knowledge acquired during the prior task can improve the acquisition of knowledge that is specific to the new task (Arzi, Ben-Zvi, & Ganiel, 1985).

As a concrete example, consider that multiplication is a component skill in both long division and exponentiation. When you learn long division, you also practice the more basic skill of multiplication, which not only reinforces your knowledge of multiplication (retroactive facilitation), but also makes it easier for you to learn how to compute exponents (proactive facilitation).

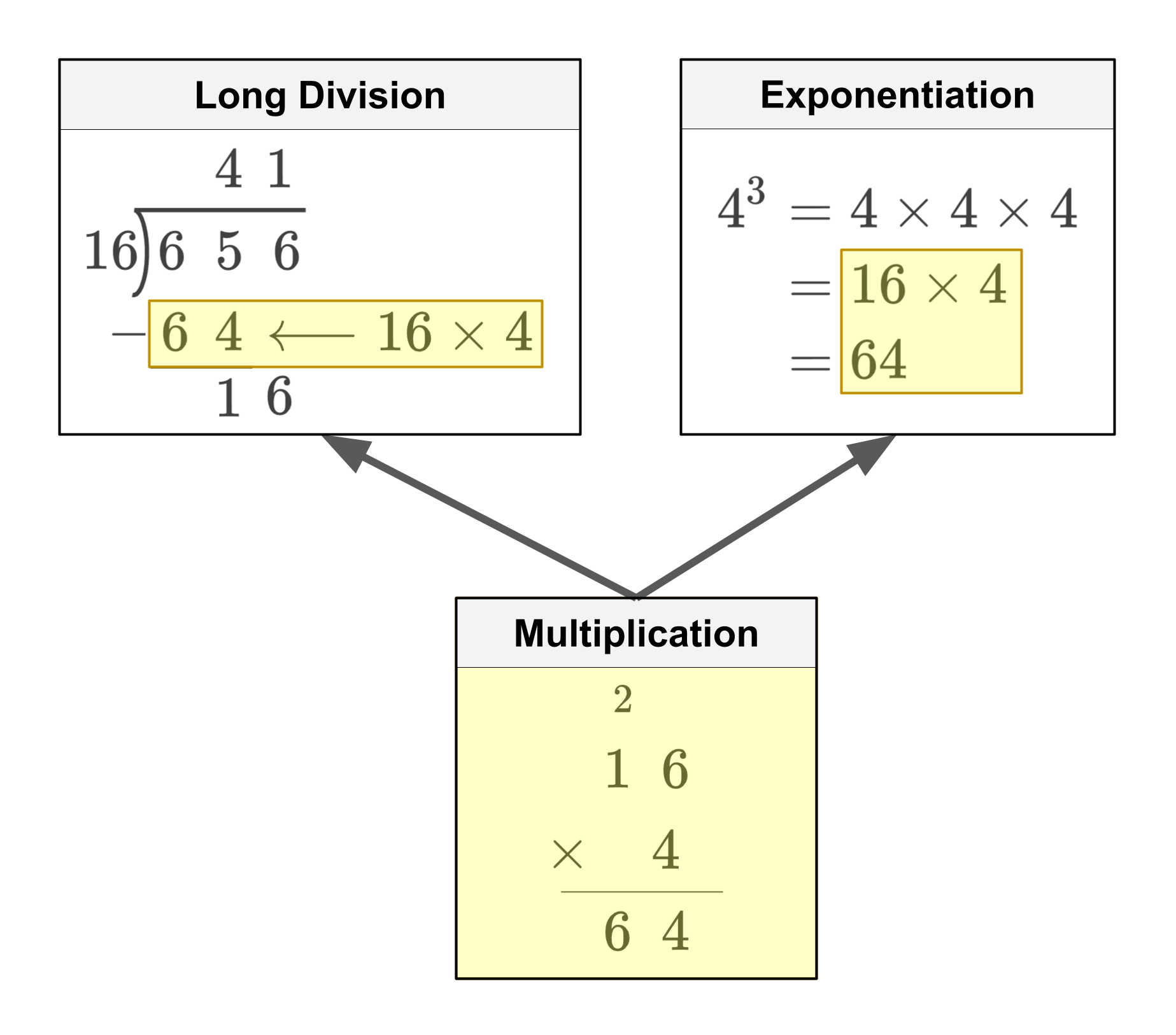
To take advantage of facilitation, it is necessary to continually layer on top of existing knowledge – that is, continually acquire new knowledge that exercises prerequisite or component knowledge. In general, the more connections (neural, cognitive, social, and experiential) there are to a piece of knowledge, the more ingrained, organized, and deeply understood it is (Cross, 1999), and the easier it is to recall via spreading activation through connections. The most efficient way to increase the number of connections to existing knowledge is to continue layering on top of it.

Structural Integrity

Layering produces structural integrity, a well-known engineering concept that also applies to knowledge (the underlying structure of one’s knowledge is known as their schema). When advanced features are built on top of a system, they sometimes fail in ways that reveal previously-unknown foundational weaknesses in the underlying structure. This forces engineers to fortify the underlying structure so that the system can accommodate new elements without compromising its integrity.

Fortifying the underlying structure often requires improving its organization and elegance, which, when applied to student schemas, produces deep understanding and insight. When the structural integrity of a system is increased, it also becomes easier to add more advanced features in general. In the same way, when the structural integrity of a student’s schema is increased, it becomes easier to assimilate new knowledge in general.

References

Arzi, H. J., Ben-Zvi, R., & Ganiel, U. (1985). Proactive and retroactive facilitation of long-term retention by curriculum continuity. American educational research journal, 22(3), 369-388.

Ausubel, D. P., Robbins, L. C., & Blake Jr, E. (1957). Retroactive inhibition and facilitation in the learning of school materials. Journal of Educational Psychology, 48(6), 334.

Cross, K. P. (1999). Learning is about making connections. The Cross Papers; 3.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.