Intuiting Limits

by Justin Skycak on October 02, 2017

The limit of a function is the height where it looks like the scribble is going to hit a particular vertical line.

This post is part of the series An Intuitive Primer on Calculus.

The limit of a function is the height, or $y$-value, where it looks like the scribble is going to hit a particular vertical line, or $x$-value – but sometimes scribbles don’t actually hit where they look like they’re going to hit.

For example, if you have a weird scribble with a broken piece removed, the limit at $x=1$ is the height where the rest of the function suggested the piece was going to hit, not the “island” segment where the piece actually hits $x=1.$

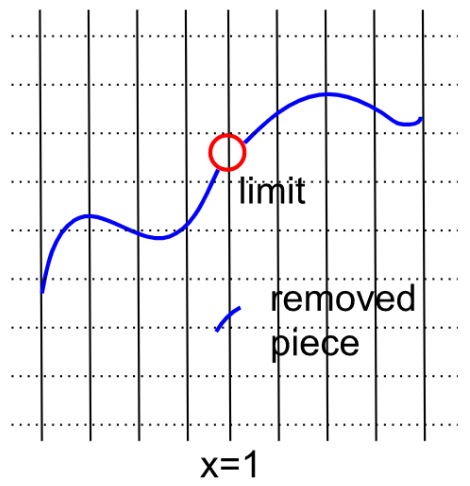
On the other hand, the function below actually occupies its limit at $x=1,$ because it hits where it looks like it’s going to hit.

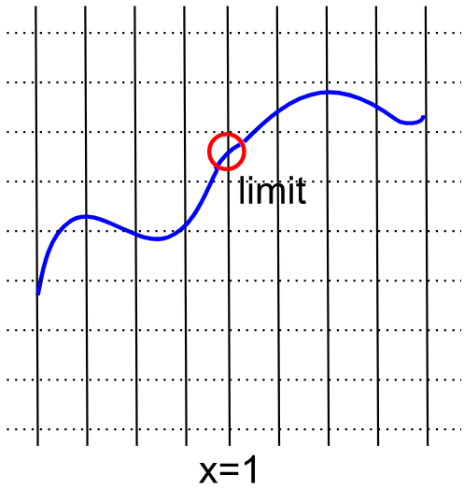
Functions that actually hit where they look like they’re going to hit, like the one above, are called continuous functions. A rule of thumb: a function is continuous if you can draw it without picking up your pen.

A faster way to find a function’s limit, without having to draw out the function, is to use the function’s equation. If the function is continuous, then all you need to do is plug the $x$-value of the limit into the function. For example, to find the limit of $x^2-1$ at $x=1,$ you can simply plug in $1$ for $x{:}$

$\begin{align*} \lim_{x\rightarrow 1}(x^2-1)=1^2-1=0 \end{align*}$

But sometimes you’re not able to plug in directly, and you have to manipulate the equation first. For example, if you try plugging in to $\lim\limits_{x \rightarrow 1} \frac{x^2-1}{x-1},$ you get $\frac{0}{0},$ which is undefined because of the 0 in the denominator. But if you manipulate the equation first, you can convert it into a form where you can plug in the limit:

$\begin{align*} \lim_{x \rightarrow 1} \frac{x^2-1}{x-1} &= \lim_{x \rightarrow 1} \frac{(x+1)(x-1)}{x-1} \\[5pt] &= \lim_{x \rightarrow 1} x+1 \\[5pt] &= 1+1 \\[5pt] &= 2 \end{align*}$

Other times, the limit might not even exist! In $\lim\limits_{x \rightarrow 1} \frac{1}{\vert x-1 \vert},$ you cannot plug in because you’ll get $\frac{1}{0},$ which is undefined. However, there is no way to manipulate the function as it is already in its most simplified form. When a limit doesn’t exist, it means there is no number the function looks like it should go to at that $x$-value.

Sometimes this just happens because a function gets infinitely high or infinitely low. To discern this from the equation, it is helpful to think of plugging in $x$-values that are very close, but not equal to, the limit value.

For example, in $\lim\limits_{x \rightarrow 1} \frac{1}{\vert x-1 \vert},$ you might try plugging in $0.999$ instead of $1.$ Then you get

$\begin{align*} \frac{1}{\vert 1-0.999 \vert} = \frac{1}{0.001} = 1000. \end{align*}$

If you try an $x$-value that is even closer, like $0.999999,$ then you get

$\begin{align*} \frac{1}{\vert 1-0.999999 \vert} = \frac{1}{0.000001} = 1000000, \end{align*}$

which is an even bigger number. The function just keeps getting higher, the closer the $x$-value gets to $1.$

The same thing happens if we approximate from the other side with numbers slightly larger than $1,$ such as $1.001$ and $1.000001.$ So even though the limit doesn’t exist, we say that the limit is infinity. That’s written as $\lim\limits_{x \rightarrow 1} \frac{1}{\vert 1-x \vert} = \infty.$

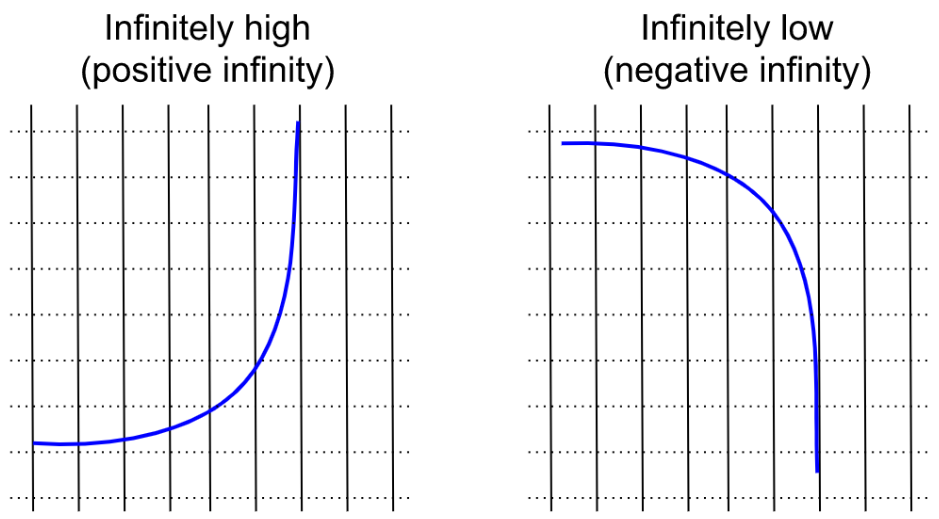
Other times, though, the limit will look like something when we approximate with numbers slightly smaller than $x,$ and something totally different when we approximate with numbers slightly bigger than $x.$ In these cases, the limit just doesn’t exist, and there’s nothing we can do about it.

For an example, consider $\lim\limits_{x \rightarrow 1} \frac{1}{1-x},$ which is like the previous example but without the absolute value signs. If we try to approximate the limit using numbers slightly smaller than $1,$ the function just keeps getting higher and higher, to positive infinity.

$\begin{align*} x=0.999 &\Longrightarrow \frac{1}{1-x}=1000 \\[5pt] x=0.999999 &\Longrightarrow \frac{1}{1-x}=1000000 \end{align*}$

But if we use numbers slightly bigger than $1,$ the function just keeps getting lower and lower, to negative infinity.

$\begin{align*} x=1.001 &\Longrightarrow \frac{1}{1-x}=-1000 \\[5pt] x=1.000001 &\Longrightarrow \frac{1}{1-x}=-1000000 \end{align*}$

Since we get two different answers depending on whether we approach $1$ from above or below, the limit does not exist.

This post is part of the series An Intuitive Primer on Calculus.