History of Calculus: The Man who “Broke” Math

When Joseph Fourier first introduced Fourier series, they gave mathematicians nightmares.

This post is part of the series Connecting Calculus to the Real World.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Taylor series allow one to write differentiable functions as infinite polynomials. Fourier series are similar, except instead of an infinite polynomial, they use the sum of infinitely many frequencies of sine and cosine waves. Fourier series have seen many applications across mathematics, physics, and engineering, but when Joseph Fourier first introduced them in the beginning of the 19th century, they gave mathematicians nightmares.

Sine and cosine are both continuous functions, so when you add a bunch of them together, the result is continuous. At the time mathematicians had not given much thought to the difference between finite sums and infinite sums, so it was assumed that if you add together infinitely many continuous functions like sine and cosine waves, the result would still be continuous.

However, this turned out to be incorrect. There is a Fourier series that corresponds to the discontinuous step function shown below.

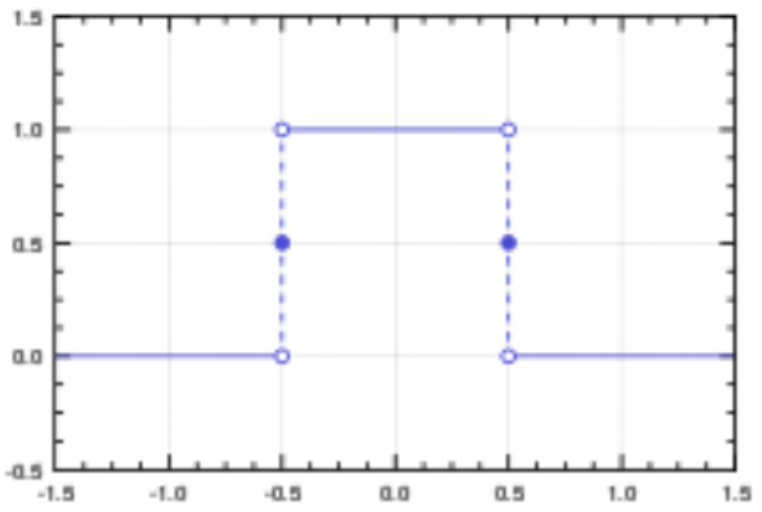
This was troubling to the mathematical community, because all work based on infinite sums was suddenly on shaky ground. Consequently, during the rest of the 19th century, there was a movement in the mathematical community to reformulate previous findings in a more rigorous fashion. This way, they could be certain that they were correct, and there would be no worrisome “surprises” like Fourier’s discontinuous series in the future.

To this end, Augustin-Louis Cauchy, Bernhard Riemann, and Karl Weierstrass reformulated calculus in what is now known as real analysis. Later on in the 19th century, Georg Cantor established the first foundations of set theory, which enabled the rigorous treatment of the notion of infinity. Since then, set theory has become the common language of nearly all of mathematics.

This post is part of the series Connecting Calculus to the Real World.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.