Graphing Rational Functions with Horizontal and Vertical Asymptotes

This post is part of a series.

The horizontal and vertical asymptotes of a rational function can give us insight into the shape of its graph.

For example, consider the function $r(x)=\frac{3x}{x-1}$, which has a horizontal asymptote $y=3$ and a vertical asymptote $x=1$.

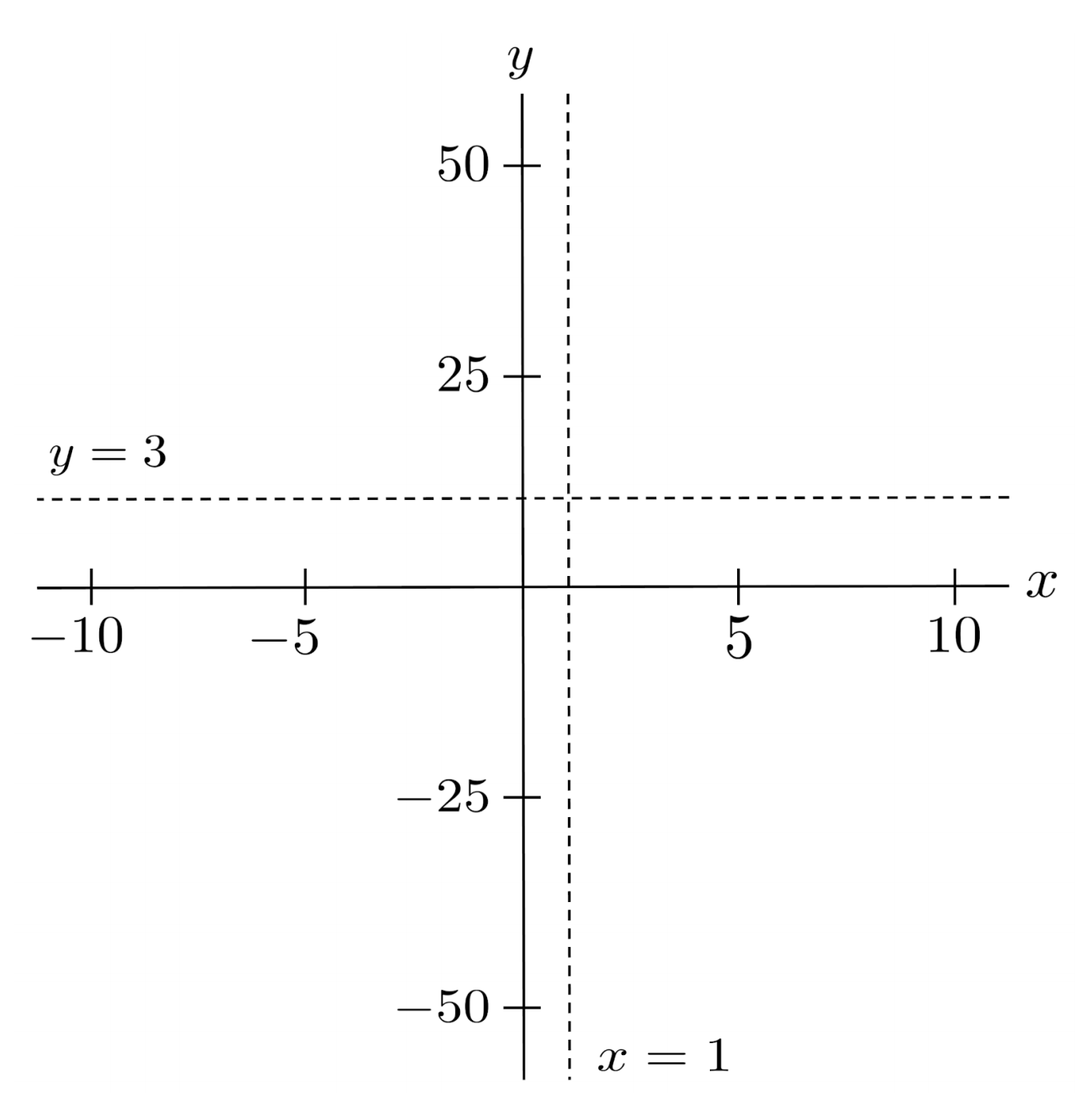
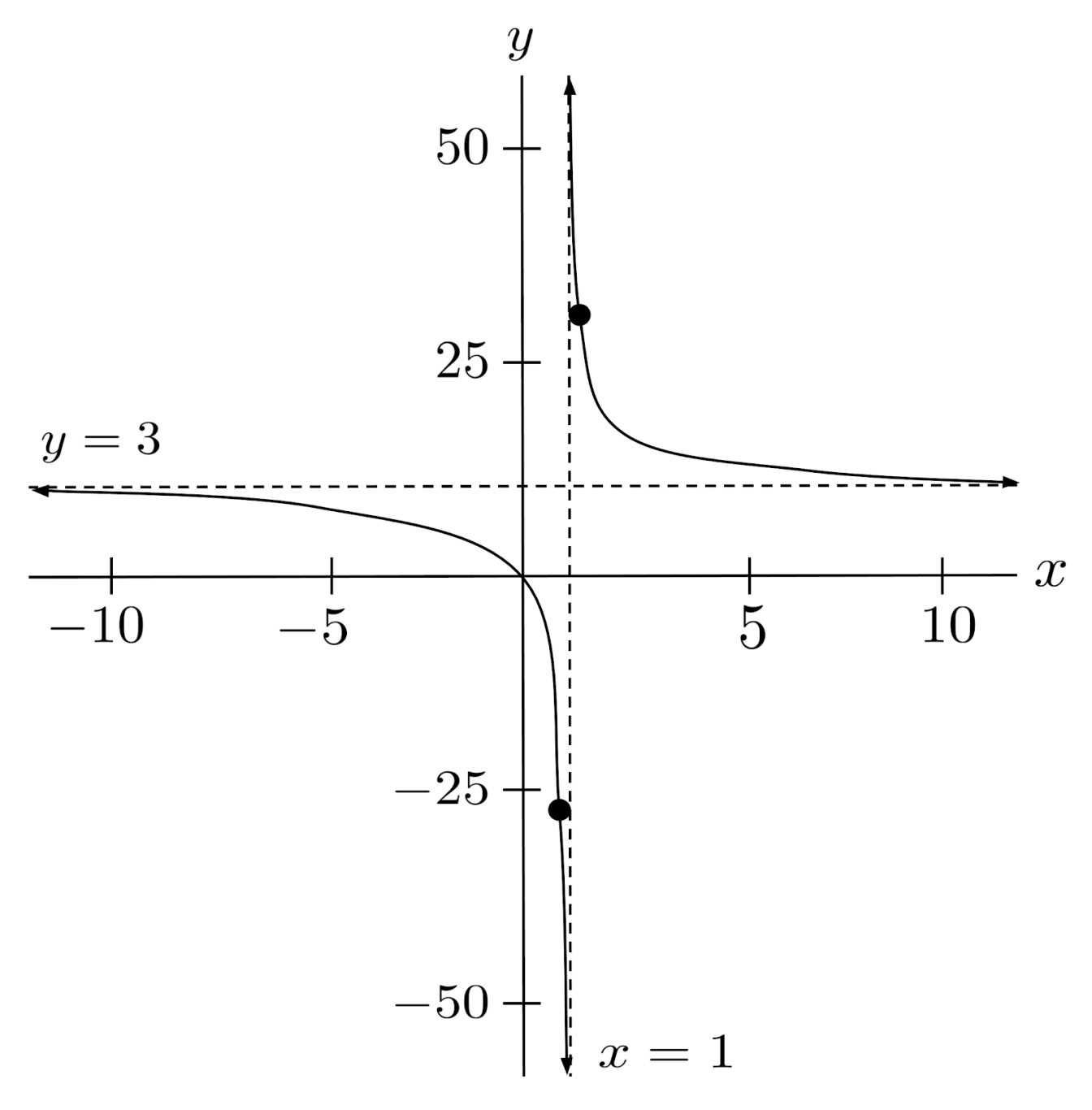
If we choose one input on each side of the vertical asymptote, we can tell which section of the plane the function will occupy.

On the left side, we evaluate $r(0.9)=-27$, which indicates the section below the $y=3$ asymptote. On the right side, we evaluate $r(1.1)=33$, which indicates the section above the $y=3$ asymptote.

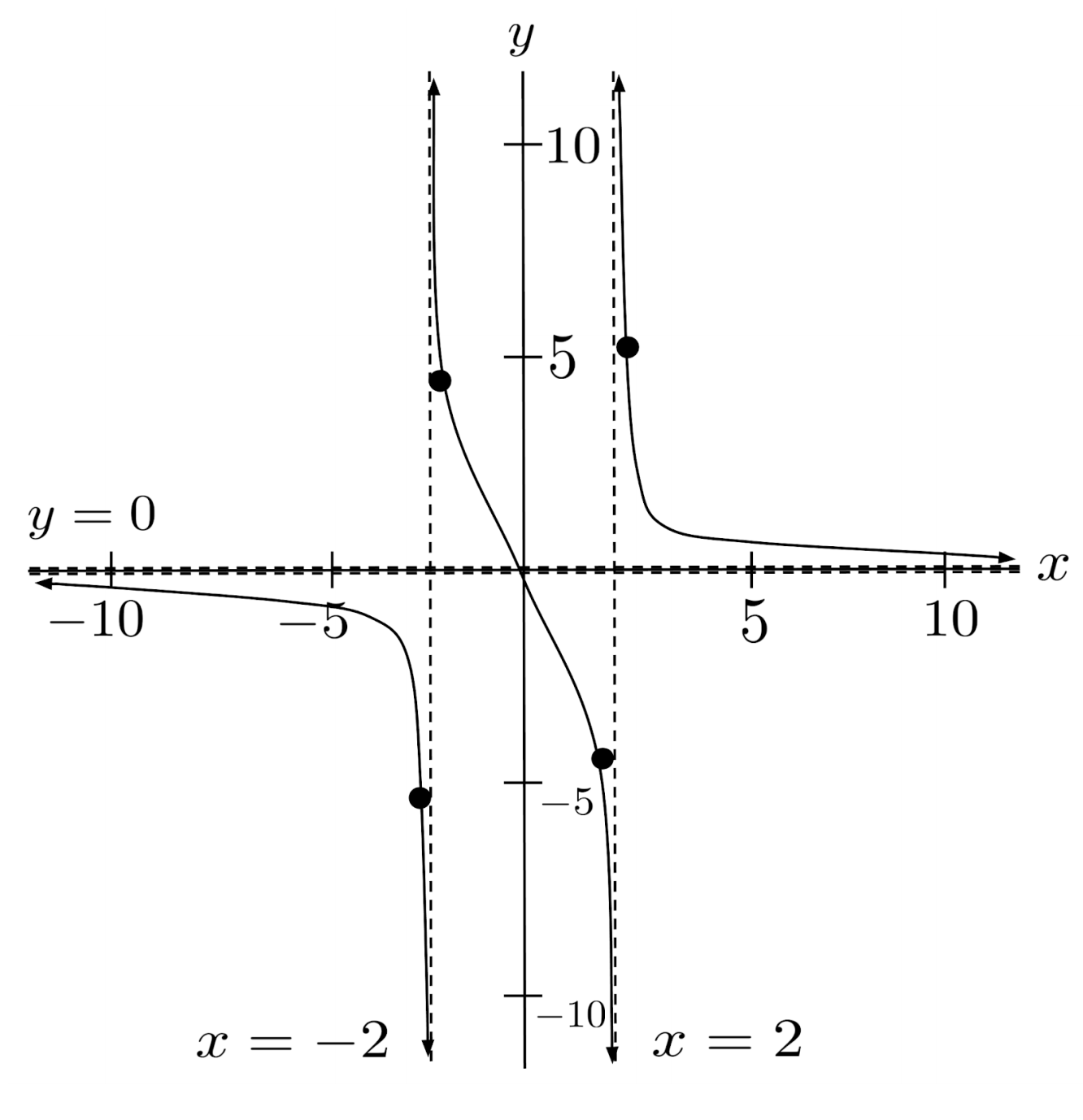
Case of Multiple Vertical Asymptotes

When there are multiple vertical asymptotes, we just have to choose test points on the sides of each asymptote.

For example, to graph the function $r(x) = \frac{x}{x^2-4}$ which has vertical asymptotes $x=-2$ and $x=2$, we can evaluate $r(-2.1) \approx -5.12$, $r(-1.9) \approx 4.87$, $r(1.9) \approx -4.87$, and $r(2.1) \approx 5.12$.

Exercises

Use horizontal and vertical asymptotes to graph the following rational functions. (You can view the solution by clicking on the problem.)

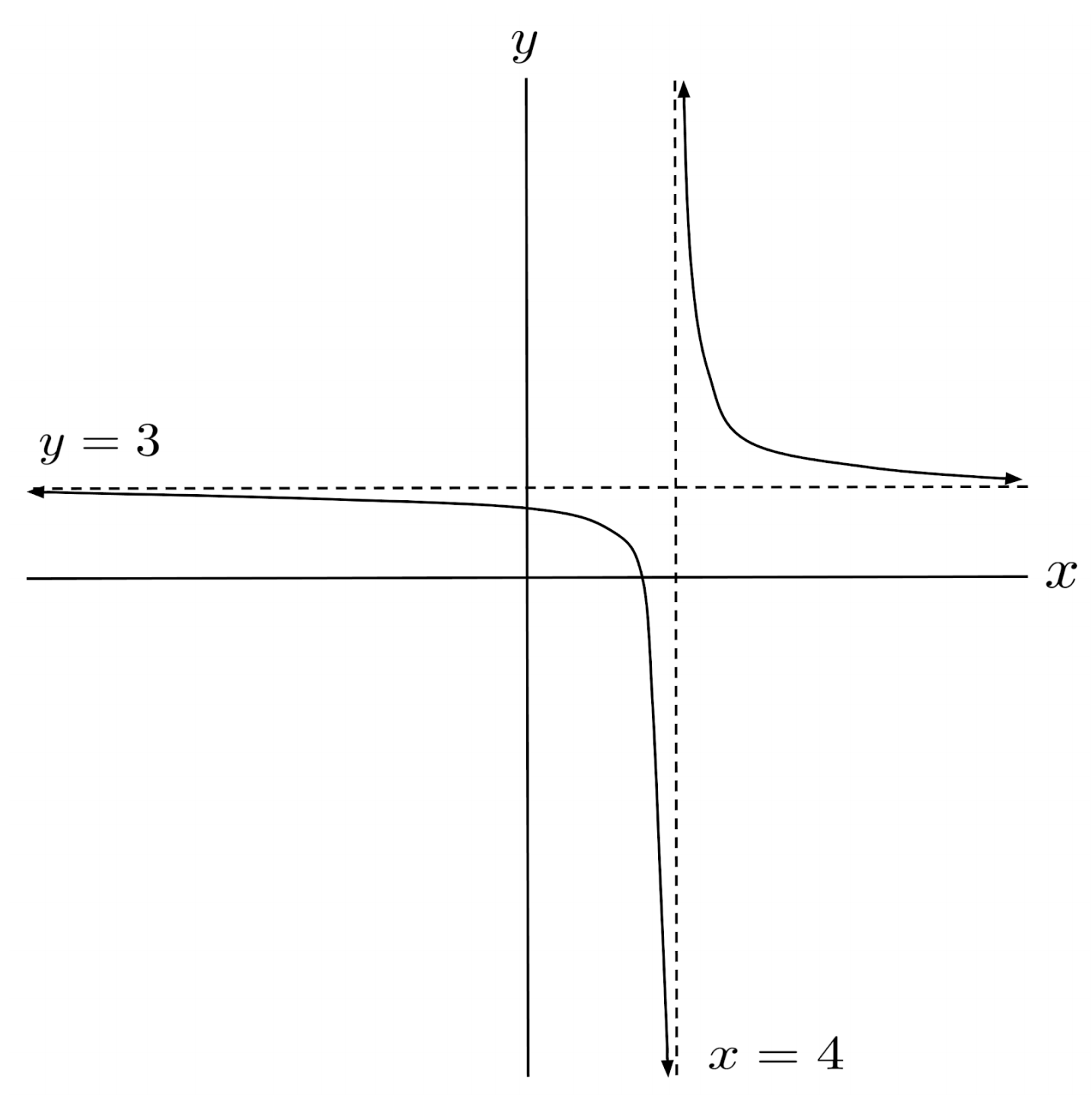
$1) \hspace{.5cm} r(x)=\dfrac{3x-10}{x-4}$

Solution:

$2) \hspace{.5cm} r(x)=\dfrac{x-4}{2x^2-9x+4}$

Solution:

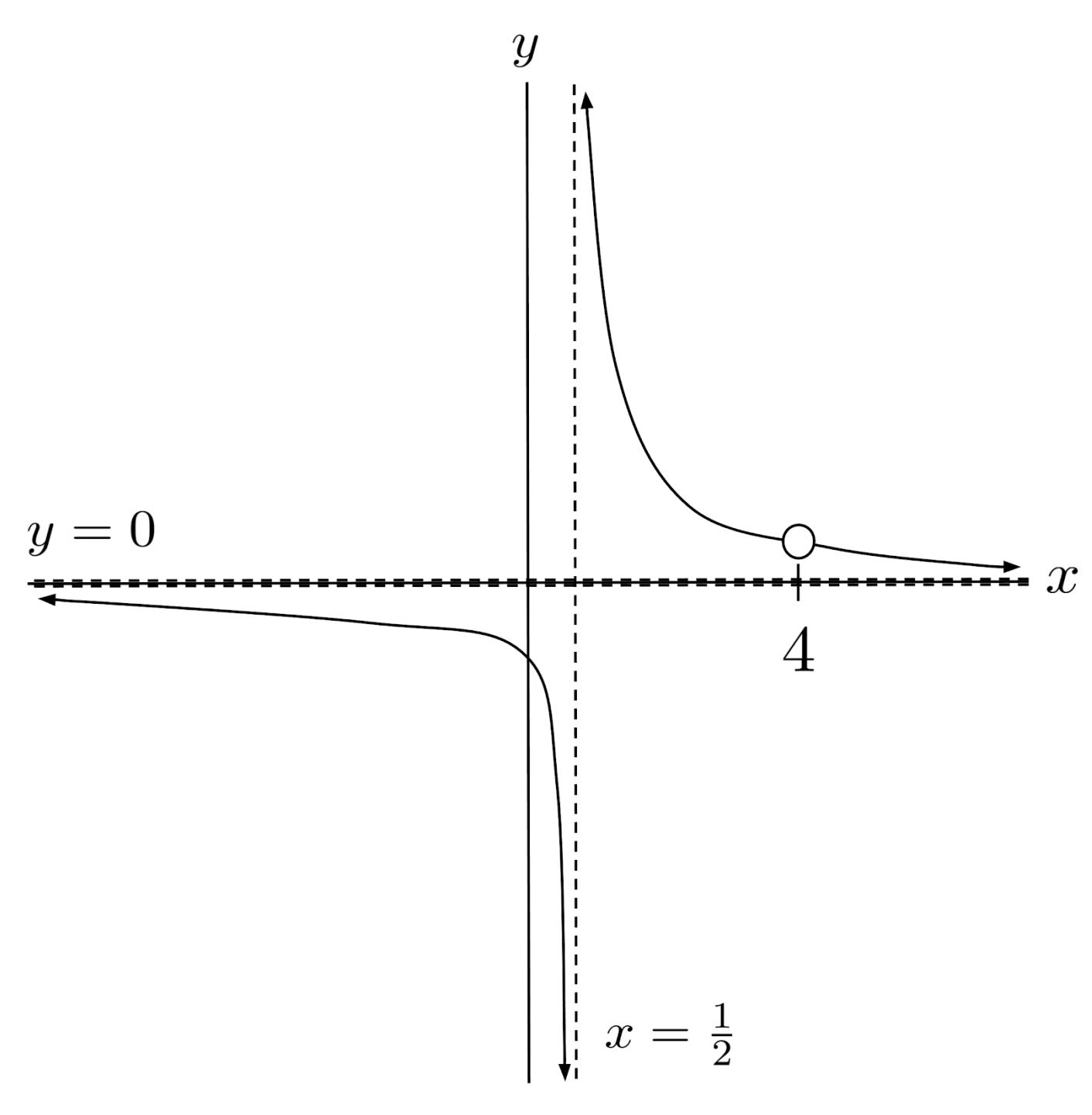
$3) \hspace{.5cm} r(x)=\dfrac{-3x^4+3x^2+x+32}{x^4-9}$

Solution:

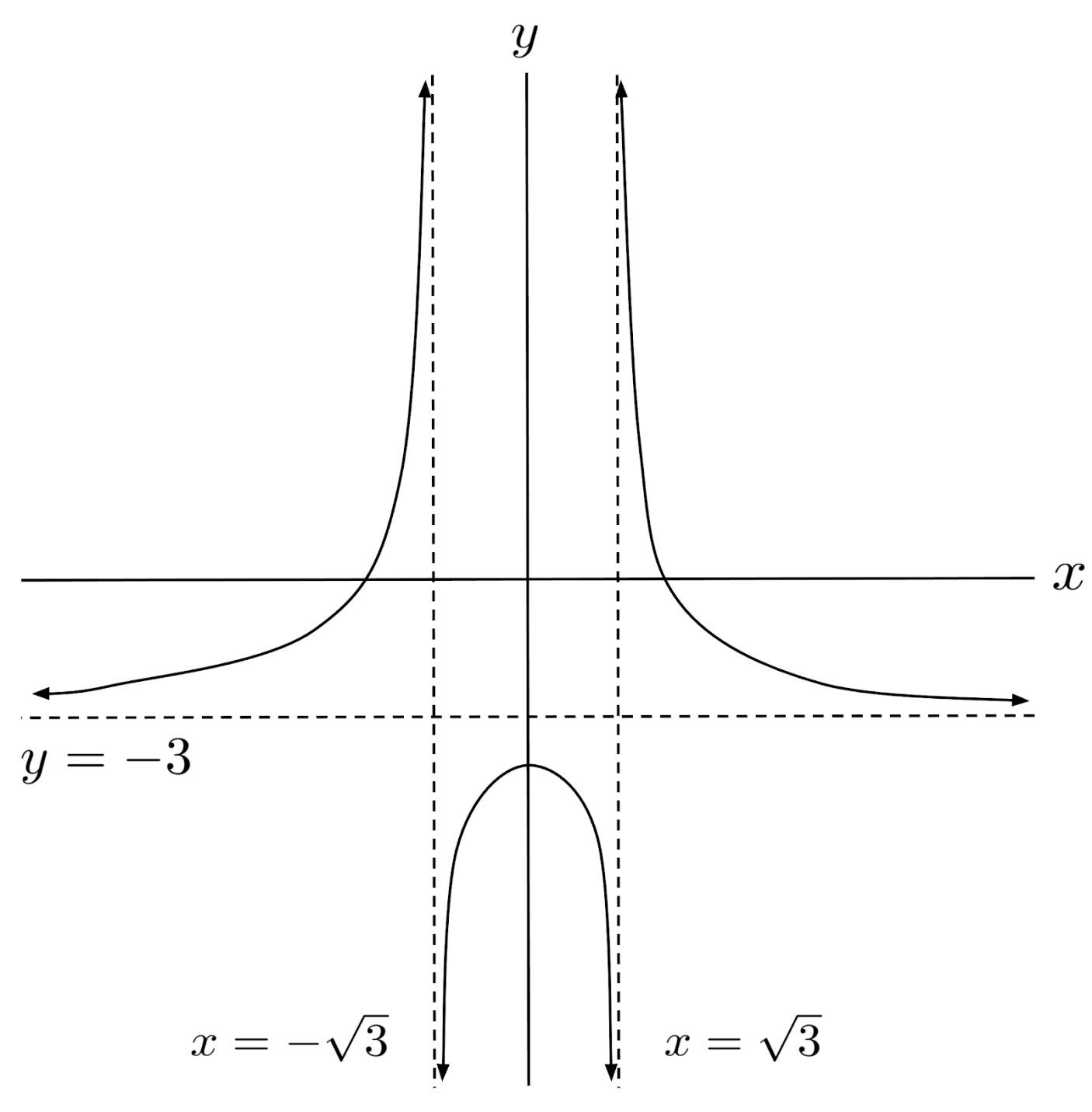
$4) \hspace{.5cm} r(x)=\dfrac{9x^5+1}{6x^5-54x^3}$

Solution:

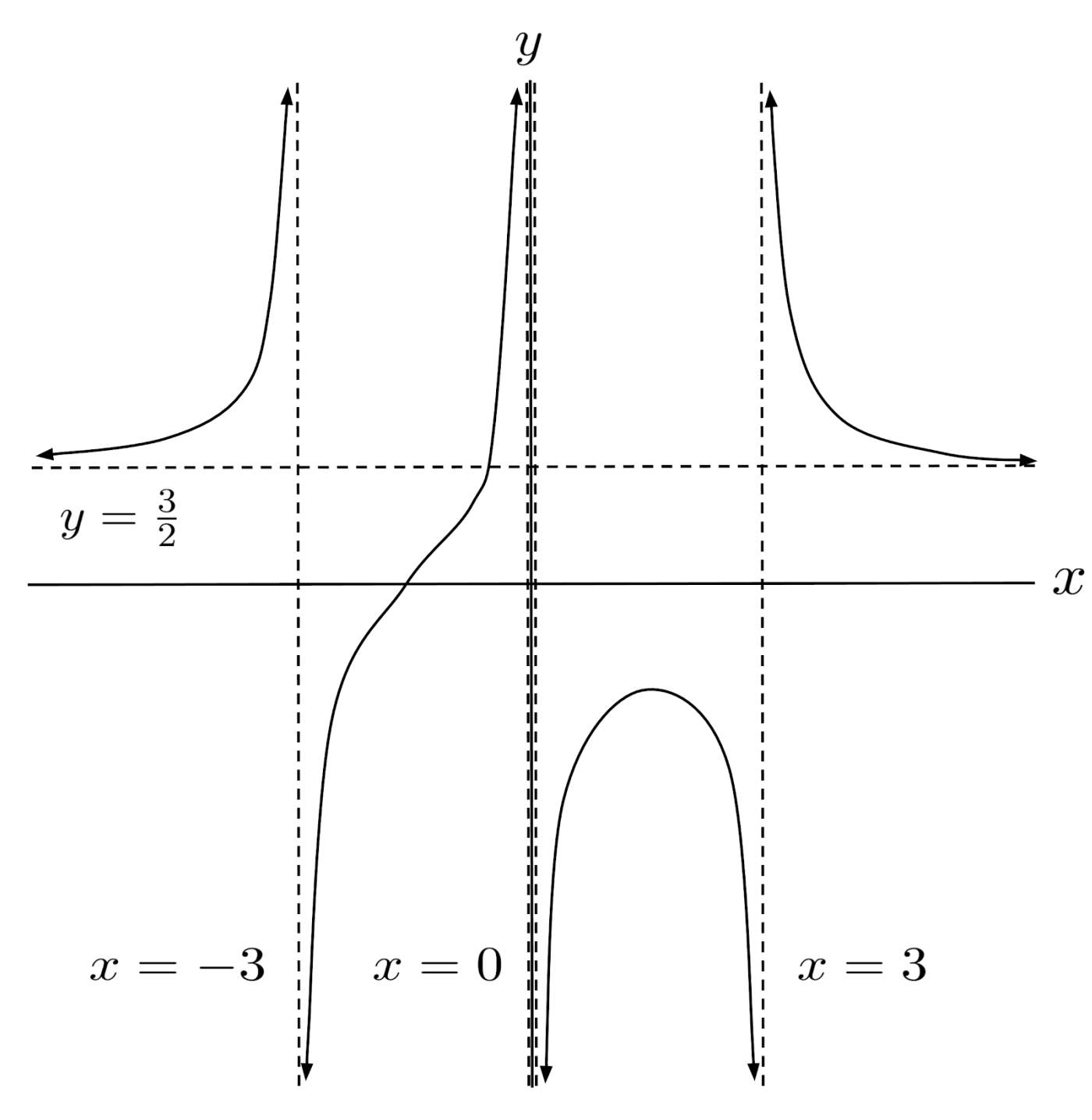
$5) \hspace{.5cm} r(x)=-\dfrac{x^3+x^2-x-1}{x^3-x^2-x+1}$

Solution:

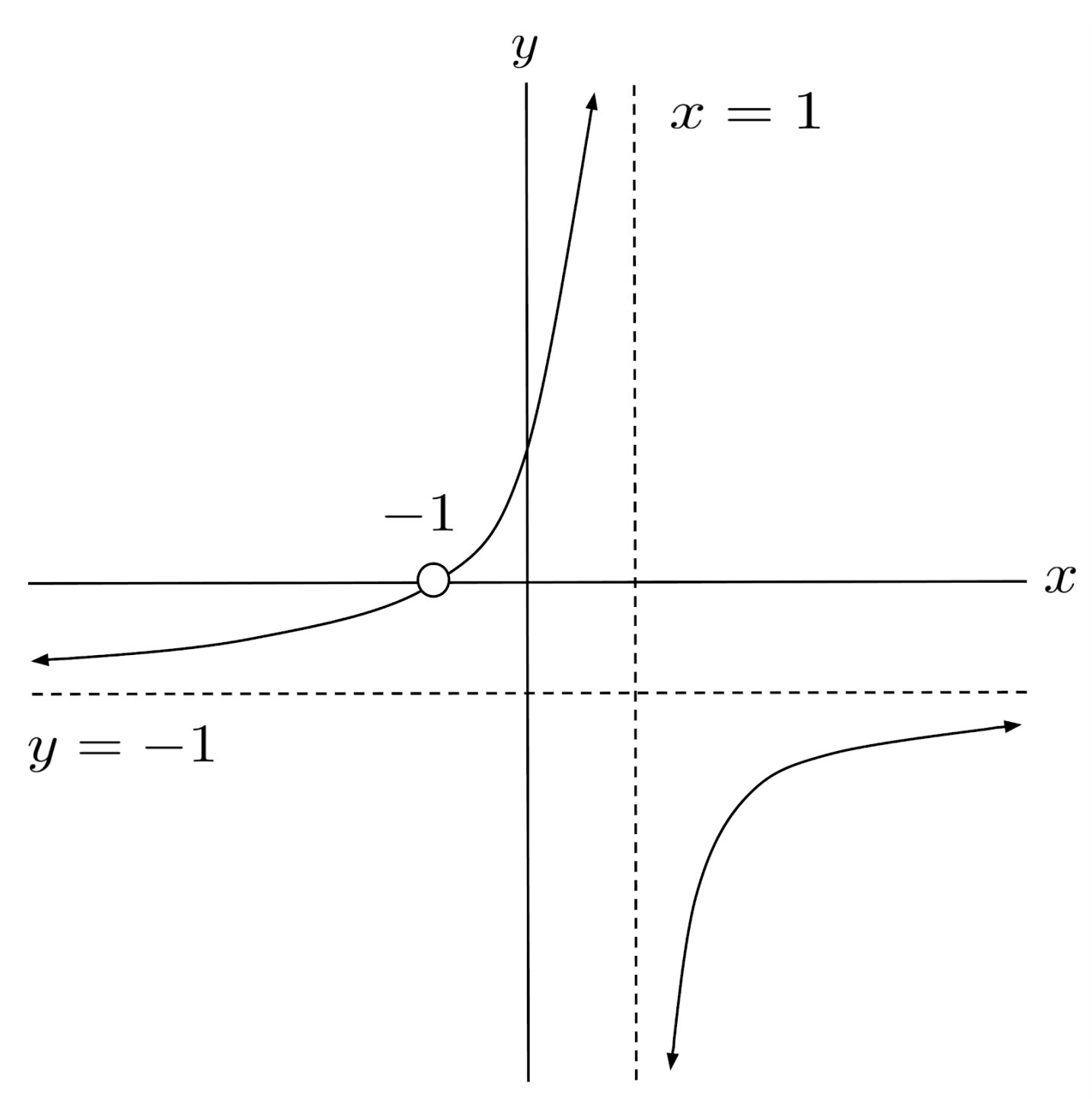
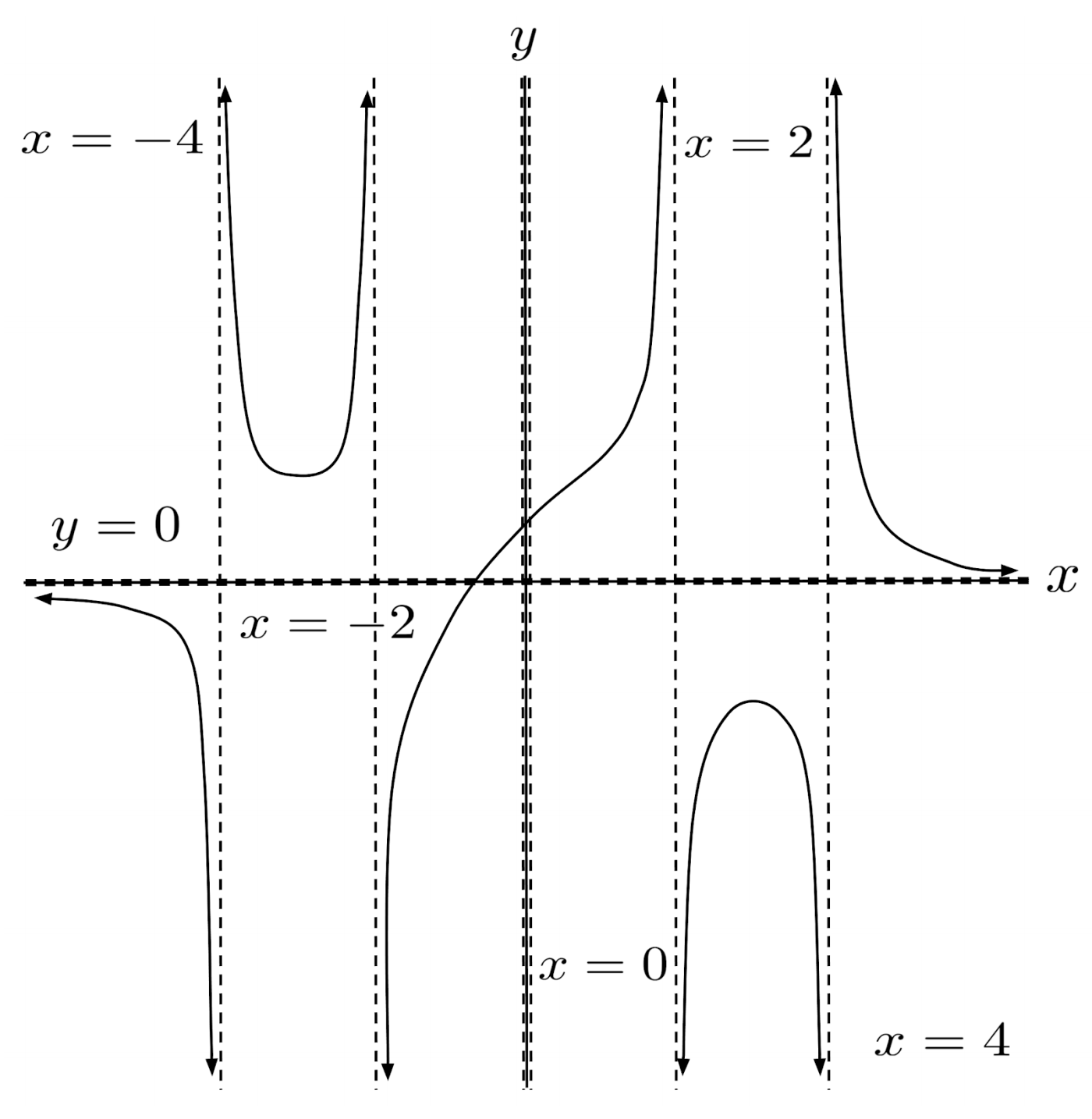
$6) \hspace{.5cm} r(x)=\dfrac{x+1}{x^4-20x^2+64}$

Solution:

This post is part of a series.