Want to Major in Math at an Elite University? Getting A’s in High School Math is Not Good Enough

If all the knowledge you show up with is high school math and AP Calculus, and you're not a genius, then there's a substantial likelihood you're going to get your ass handed to you.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Prospective math majors often graduate high school with A’s in their math classes, leading up to AP Calculus BC in their senior year, thinking that they are prepared for their university’s math program.

But if you’re trying to major in math at an elite university that is known worldwide for its math program (MIT, Caltech, UChicago, etc.) – and all the knowledge you show up with is high school math and AP Calculus, and you don’t have far outsized aptitude – then there’s a substantial likelihood you’re going to get your ass handed to you.

Here’s why this happens.

The problem is that high school math – even the “honors” track, even getting a 5 on the AP Calculus BC exam – often doesn’t accurately depict the level of background knowledge (especially proof-writing ability) that is assumed in serious math-major courses.

There are two overlapping groups of students who succeed in top math programs:

1. students who have far outsized aptitude,
2. students who have far outsized background knowledge.

For instance, it is not uncommon for elite university admits who are serious about majoring in math to graduate high school

• having already taken linear algebra & multivariable calculus, and
• having already received plenty of exposure to proofs including inklings of real analysis (e.g., epsilon-delta limit proofs) and abstract algebra (e.g., structure of the additive & multiplicative groups of integers).

These students make up such a tiny slice of the overall student population that you’re unlikely to encounter them as classmates in high school. But they exist, and they’re going to be concentrated in the math-major math classes at these elite universities.

Much of the content – or, at least, the overall way of thinking about it – will be familiar to them, and as a result, they’ll have a far outsized ability to keep up with fast-paced, poorly-scaffolded instruction, even if they’re not actual geniuses.

If you’re not able to do the same, then the class is not going to slow down just for you. You’ll likely feel dumb, like everybody is way smarter than you (when in fact only some are and the rest are just better prepared), and that will likely deliver a severe hit to your motivation.

Basically, it’s like you get accepted to some world-class martial arts training program on the basis of meeting some relatively low threshold of baseline fitness.

You show up thinking you’re prepared, but as soon as you get there and step onto the mat you get thrown clear across the room by people who were far more prepared.

Here’s a case study.

I recently had a conversation with someone who majored in physics at UChicago.

He initially started in math, and he thought he was prepared having aced AP Calculus BC, but he got smacked in the face by the level of abstraction and proof-writing ability that was assumed, and he couldn’t keep up with his classmates who had already done proofs while taking even MORE advanced courses in high school. So he switched to physics where

• proofs were less frequent, and
• the playing field felt more level in terms of how much prior knowledge was assumed (as well as how much prior knowledge other students were coming in with).

He would have liked to study math if he had more time to catch up, or if he knew earlier about how far behind he was – but he did great in all his high school math classes, and was recognized as one of the “smart kids” in the class, so he never suspected he was actually behind the curve.

Zooming out, this case study is representative of a general phenomenon that can sneak up on you when you’re at, say, the 99th percentile of a skill.

At first, you’re exceptional enough that you receive praise from virtually everyone, and you may never go head-to-head with someone who can beat you.

That is, until you join some specialized program where everyone is at the 99.9th percentile – where, suddenly, you’re the worst one there.

And here’s the real kicker: the more you have to catch up on, and the less time you have to do it, the more likely you are to hit your breaking point and fall off the rails.

Now, don’t get me wrong – even if there is a large skill gap, it is typically possible to make it up by working hard and smart. I’m not suggesting to give up. You have agency and you should exercise it.

But you also have to recognize and respect that you also have a breaking point. The less cognitively advantaged you are, the higher volume of work there’s going to be. The less time you have to do that work, the more intensely you’ll have to work. The less motivation you have to learn the subject, the less volume and intensity of work you’re going to stomach before you break and pursue alternative endeavors.

The silver lining: the better you prepare yourself during periods when there is more ample time, the more likely you are to make it across the transition zones where the expectations of your commitment and ability suddenly ramp up.

So… how do you prepare?

Given how much room for improvement I see in math education, given how many times I’ve seen students (including friends, family members, and even ourselves at some point or another) get screwed over by missing prerequisites that nobody told them about, and given how much positive impact that creates in people’s lives, my career has become centered around helping people identify and fill in prerequisite knowledge that they’re missing.

There’s a course that all of us at Math Academy have poured our hearts & souls into to help students stick the landing in their transition to intense proof-based mathematics: Methods of Proof (MoP).

MoP covers so many different types of proofs, in so many different contexts. You see the whole zoo and develop tons of experience with elementary concrete examples that get built upon in all those branch-off subjects like real analysis & abstract algebra.

Epsilon-delta limit proofs, structure and operations in the additive & multiplicative groups of integers modulo N, you name it.

Even more niche stuff like number theory – for instance, MoP covers modular arithmetic & linear congruences really comprehensively, which is another one of those things that students typically don’t learn well enough before taking a number theory course.

Anyone who takes MoP before university should feel a seamless transition into serious math-major courses, as opposed to the massive shock & overwhelm that typically occurs.

Seriously, if every aspiring math major took MoP the summer before heading off to university I bet it would cut the math major drop rate by more than half.

The Overall Takeaway

The intended message of this post is: “here’s what you’re up against, telling you now so you can prepare & avoid falling through the cracks, or if that’s already happening, you can understand that what you’re fighting may just be missing prereqs, doesn’t mean you’re dumb.”

Stated more explicitly and extensively:

Let’s be honest with students about where they stand relative to the caliber of skill they hope to join, not just the caliber of skill in their current peer group.

Let’s not tell students they’re well prepared, when in fact there is some helpful background knowledge that many future peers will come in with, that they themselves don’t have.

While it’s never pleasant to be told that you’re accumulating a knowledge deficit and are going to need to put in extra work to catch up later, the psychological gut-punch gets much softer the earlier it’s detected and delivered, and the less likely it is to become a knock-out blow.

If students don’t find out where they stand relative to the caliber of skill they hope to join, until they actually join, then there will likely be a sizeable skill gap, and they likely won’t realize that a sizeable portion of that skill gap can be attributed to the outsized background/training of their new peers.

If there is a sizeable skill gap, then the student will likely struggle and feel like there is a gigantic gap between them and their classmates. They will likely think everybody is way smarter than them, when in fact only some are, and the rest are just better prepared.

Struggling students often do not realize that missing prerequisite knowledge is the source of their struggle (which is not surprising, since it’s knowledge they don’t know). They often don’t realize that they can catch up, and if they do, they often don’t know how to catch up. Even if they put tons of time/effort into studying, if the skill gap is large enough and the material too advanced relative to their level, then the study may be ineffective and they may not catch up even with their best effort.

Years later, after accumulating some life experience, they may reflect and realize what happened – but in the moment, when they’re young and in the thick of it, they’ll likely just think they’re too dumb.

Don’t get me wrong, even if there is a large skill gap, it is typically possible to make it up by working hard and smart. You have agency, but you have to recognize and respect that you also have a breaking point. The less cognitively advantaged you are, the higher volume of work there’s going to be, the less time you have to do that work, the more intensely you’ll have to work, and the less motivation you have to learn the subject, the less volume and intensity of work you’re going to stomach before you break and pursue alternative endeavors.

Lots of people like to act as though they’re invincible and infinitely motivated, and lack of preparation has no effect on outcomes, only the amount of work necessary to achieve them. They act this way because they so desperately want this to be true and have never had the experience of hitting a breaking point. But, realistically, the likelihood of an outcome decreases with the intensity and duration of work necessary to achieve it, especially when they are high to begin with.

(It’s like cognitive load. Even if you know what you’re doing, your error rate skyrockets under heavy cognitive load, no matter how hard you try. You can exercise your agency to avoid cognitive overload, but you can’t exercise your agency to “overcome” it. You can exercise your agency to avoid falling off a cliff, but if you’re already falling, can’t exercise your agency to overcome the impact.)

To recap: everybody has a breaking point, and that breaking point is different for different people, and the thing that keeps you far away from the breaking point is being prepared, not experiencing an insanely high spike of pressure to learn a gigantic amount of material in a tiny amount of time to catch up. The better you prepare yourself during periods when there is more ample time, the more likely you are to make it across the transition zones where the expectations of your commitment and ability suddenly ramp up.

What’s in everyone’s best interest is to be honest with students about where they stand. E.g., if a kid is potentially aspiring to major in math at an elite university, let’s make it clear to them that many of their peers are going to come in mathematically “bulked up” well beyond AP Calculus, and encourage them to do the same.

Because, on average, the more prepared they are, especially leading up to the main bottleneck points in their talent development journey, the less likely they will be to fall off the rails, and the further they will be able to go in their preferred talent domain.

Stories

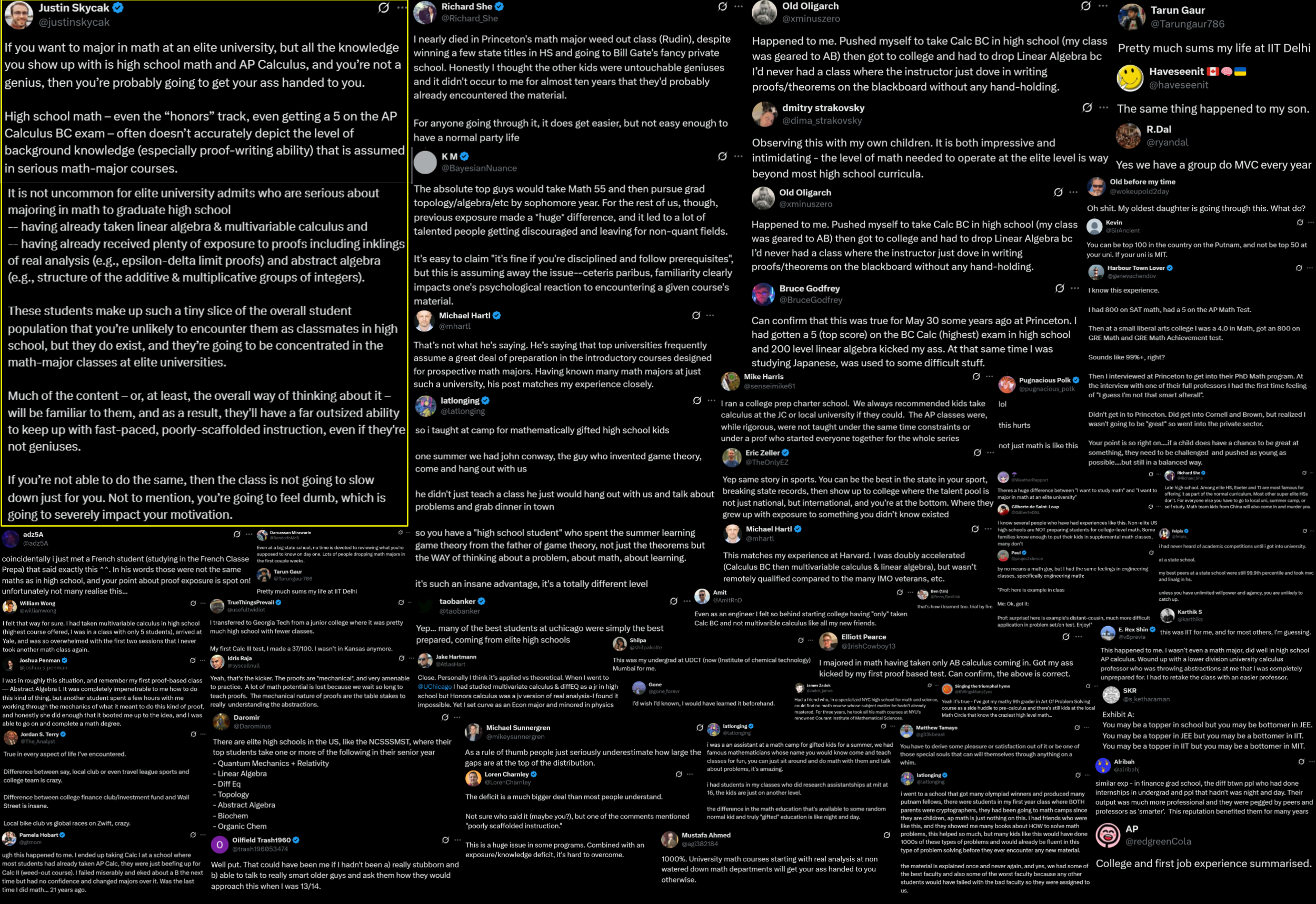
A snippet of this post blew up on X, and tons of interesting stories emerged in the comments, from people who thought they were well prepared for elite university math courses after having completed the standard HS math curriculum, only to get smacked in the face, rug pulled out from under them, and realize (often much later) that they were actually missing lots of prerequisite knowledge.

(And also stories from people who have seen drastic differences in students’ mathematical preparation at the elite level.)

Some of my favorites:

A fuller compilation:

A reader summed up the overall takeaway pretty well: “I liked how the comments were evenly split between ‘this is nonsense’ and ‘this was me.’”

Indeed, there’s a very strong survivorship bias. It’s amusing how many people who didn’t experience it themselves can’t imagine it happening to others.

Also some people of far outsized mathematical upbringing, who don’t even realize how atypical their experience was. E.g., some guy was arguing that you see epsilon-delta proofs in a typical honors calculus course in high school, which is just completely false, in the US at least.

And of course plenty people of far outsized mathematical aptitude, who don’t have a good frame of reference for how well a more typical student can identify and spin up on missing prerequisite knowledge.

Which is, amusingly, one of the primary reasons why the phenomenon happens in the first place. Lots of math instructors (esp. at elite universities), being of far outsized aptitude and often having far outsized mathematical upbringings, don’t have a good frame of reference for what high school math covers is or how well non-genius students can identify and spin up on missing prerequisite knowledge.

Follow-Up Questions

Q: Sounds like he just didn’t have enough curiosity. I think these kinds of students have abundant practice with the mechanics but not as much with questioning, “why?” while fumbling in the dark with abstraction.

A: That’s the complete opposite of what happened. Unlike their classmates, this student barely had any practice with the mechanics of proof-writing. Curiosity drew the student to math but lack of mechanical skills (too big a gap to fill in to short a time) pushed them out.

Q: Why didn’t this guy just bunker down and fill in his prerequisites?

A: The student often doesn’t understand that missing prerequisite knowledge is the primary source of their struggle, or what that specific prerequisite knowledge is, or how to go about filling it in.

When a student is missing prerequisites, it often doesn’t occur to them until many years later, if at all.

It’s one of those things that gets easier realize as you get older and accumulate more life experience, especially if you end up working with youngsters in a skill development setting.

But when you’re young and in the thick of it, it’s hard to understand what’s really going on. In the moment, you just think you’re too dumb.

As Richard She described: “I nearly died in Princeton’s math major weed out class (Rudin), despite winning a few state titles in HS and going to Bill Gate’s fancy private school. Honestly I thought the other kids were untouchable geniuses and it didn’t occur to me for almost ten years that they’d probably already encountered the material.”

Q: What if you take an intro to proofs class at a local college or university during high school, before you enter a college math major? Will that solve the problem?

A: I think it’s rare to find an Intro to Proofs course that is simultaneously

1. comprehensive enough to make a seamless transition to higher math, while remaining
2. scaffolded enough to be accessible to students with absolutely zero proof-writing experience.

Not saying it can’t happen – just that, if a student signs up for an Intro to Proofs course at a local university, then it’s not necessarily a guaranteed solution as one would hope.

Personally, I took an Intro to Proofs course at a local community college while in high school, and it didn’t cover nearly enough material as I would have hoped. I didn’t end up learning much from it.

And at the same time, I’ve heard of students getting introduced to proofs at a more serious university and getting completely blown out of the water (even though the whole purpose of explicitly introducing students to proofs is to avoid doing that).

Cost is another factor: the reason why I took Intro to Proofs at my local community college was because it would have cost thousands of dollars to take a class at the more serious university in town. Even the community college class was painfully pricey – still well into the multiple hundreds of dollars.

Q: Yep same story in sports. You can be the best in the state in your sport, breaking state records, then show up to college where the talent pool is not just national, but international, and you’re at the bottom. Where they grew up with exposure to something you didn’t know existed.

A: Exactly. Initially you think you’re training hard & smart enough to max out your potential.

Then you get to high enough level to realize that, while a few people there do have more inborn talent than you, many of them have no inborn edge over you – but they’re way ahead because they trained harder/smarter than you originally realized was possible (typically because they grew up with chance exposure to it from some adult in the know).

And if you had known that was possible years ago, you could have capitalized on it and come a lot further.

Q: Is this post supposed to be demoralizing?

A: I don’t mean to demoralize anyone. Nobody should give up on a dream if they’re making progress, even if their starting point is relatively behind.

What I’m trying to convey is something positive and empowering: how to better prepare to better guard yourself from falling through the cracks, which happens quite often. I want to see students succeed, and if a student is accumulating a deficit and is going to need to catch up later, they need to know that earlier.

What’s demoralizing is to give students the impression they’re well prepared, when in fact they’re about to have the rug pulled out from under them.

Getting a rug pulled out from under you (because you’re missing prerequisite knowledge that nobody told you to spin up on) is one of the most demoralizing things that can happen to you as a student, because in the moment, in the thick of it, you likely don’t realize that missing prerequisite knowledge is the source of your struggle. You just think you’re dumb.

Q: That didn’t happen to me. I majored in math at (insert elite college here) with only high school AP classes under my belt. I’ve a talent for math but I’m no genius.

A: I’m glad that it didn’t happen to you. Unfortunately, it happens to a lot of other people. As others have noted, the reactions to the post are evenly split between “this is nonsense” and “this was me.”

Many people of far outsized mathematical upgringing don’t even realize how atypical their experience was. E.g., some guy was arguing that you see epsilon-delta proofs in a typical honors calculus course in high school, which is just completely false, in the US at least.

And of course plenty people of far outsized mathematical aptitude don’t have a good frame of reference for how well a more typical student can identify and spin up on missing prerequisite knowledge.

These are, amusingly, some of the primary reasons why the phenomenon happens in the first place. Lots of math instructors (esp. at elite universities), being of far outsized aptitude and often having far outsized mathematical upbringings, don’t have a good frame of reference for what high school math covers is or how well non-genius students can identify and spin up on missing prerequisite knowledge.

Q: Was this your experience at Notre Dame?

A: Not at all. I self-studied most of a standard undergrad math degree during high school and came in exceedingly well prepared.

I pushed myself to take the hardest classes I could get into (including senior-level topology in the first year & grad courses the second year), but the standard classes required for the major were an absolute breeze.

But I did get to know a math major classmate who had no exposure to math beyond AP Calc BC coming in, who struggled to pick up proofs on the fly and ultimately dropped.

Q: Why aren’t these elite schools more straightforward about their expectations and reasonable prerequisites?

A: Lots of math instructors at elite universities, being of far outsized aptitude and often having far outsized mathematical upbringings, don’t have a good frame of reference for what high school math covers is or how well non-genius students can identify and spin up on missing prerequisite knowledge.

Q: I can believe this at a top ~5-7 school (MIT, Harvard, Princeton, etc.). I’m skeptical this would be true at, say, the 15th through 25th schools, etc. Say, Vanderbilt, Notre Dame, WashU, Emory, etc.

A: Yes – that’s why I specified “elite university” in the post. Much more common there than at “great universities” where the pace of instruction is not as insanely fast, though it can still happen. (E.g., even at Notre Dame, I did get to know a math major classmate who had no exposure to math beyond AP Calc BC coming in, who struggled to pick up proofs on the fly and ultimately dropped.)

Q: Isn’t it healthy to get an ego check from time to time? There’s nothing wrong with having to work hard to catch up.

A: Ego checks are fine. What’s not fine is when students are given the impression they’re well prepared, when in fact they’re about to have the rug pulled out from under them. If they’re accumulating a deficit and are going to need to catch up later, they need to know that earlier.

Q: Are you saying that mastering proof techniques automatically makes someone a genius?

A: Having that doesn’t make someone a genius, but lacking that often causes non-genius students to drop their math major.

Q: Wouldn’t he have covered epsilon-delta proofs if he had taken the honors math classes in high school?

A: No. Not in the US at least. Most high schools top out at AP Calc BC, no epsilon-delta, no proofs at all beyond the most basic two-column geometry proofs.

AP Calc BC is considered the highest honors calculus course at basically every high school in the US that offers it.

It sounds like you’re thinking of university math programs and assuming that high school is the same. It’s very different.

Q: This never happens to me. Unlike the student in your story, I have strength, willpower, and will never give up. I don’t have a breaking point. That is the difference between mediocrity and greatness.

A: I understand how invincible it makes you feel to be the cognitive and motivational standout in your peer group. I hope that one day you can experience what most other students go through and be less cocky to them.

Q: It’s hard to believe a single anecdote generalizes.

A: I see this sort of thing all the time. Here’s another story of this phenomenon, getting one’s ass handed to them in elite university math courses due to missing prerequisite knowledge, despite acing all their high school math courses through AP Calc BC:

I know a Caltech grad whose first year math class (that they placed into on the basis of AP or placement test credit or whatever) asked them to do proof by induction on graphs (the vertices/edges kind).

Although the course covered a bit of proof by induction in the setting of algebraic expressions beforehand, the jump into the graph setting was very rapid and there was little explicit practice with graphs beforehand. There was an implicit assumption that students were already comfortable working with graphs or would spin up on the fly.

Instructor: “Ok class, now that we did a few problems on induction, I want you to do this next induction problem on a graph. This is a big leap in generalization/technique and it will really showcase the power of induction.”

Student: “WTF is a graph? Vertices & edges? Trees, cycles? Topological equivalence? Didn’t learn about any of that in high school.”

Instructor: “Don’t worry, vertices are dots and edges are lines. Now you’re all spun up. Hope you enjoy the problems!”

Student: ????

Unsurprisingly, the student ended up failing the course.

Now, whether you want to chalk that up to missing prerequisites, or the university failing to place properly and instructors failing to assess early and communicate to students who should drop, the conclusion is the same: the student fell through the cracks, and more extensive prerequisite knowledge would have avoided or at least mitigated the situation.

Q: (follow-up to question above) It sounds like they took a class which was too advanced for them, or else they weren’t willing to put in the same work everyone else was.

A: You’re not getting the point.

Obviously the class was too advanced for them – they were missing prerequisite knowledge, but they didn’t realize it until years later. They put tons of time/effort into studying, but the material that was too advanced for them, so it was ultimately ineffective.

The student wasn’t being pointed in the right direction by the advisors and profs who were being paid to guide them. Some rules from teaching 101:

1. You don't point a student at a course that's too advanced for them.
2. You assess early so you can tell if there's been a mistake and you've got students who are out of their depth.
3. You communicate to those students that they need to switch to a less advanced course.

The student got screwed over twice:

1. They weren't given a heads up about any additional prerequisite knowledge outside a typical HS curriculum through AP Calc BC.
2. They were guided into a course too advanced for them and not guided out of it.

And when a student is out of their depth, especially in an entry-level course, they often don’t understand that missing prerequisite knowledge is the primary source of their struggle, or what that specific prerequisite knowledge is, or how to go about filling it in.

That realization often doesn’t occur until many years later, if at all. In the moment, in the thick of it, they’ll likely just think you’re too dumb.

They can put tons of time/effort into studying, but if they’re studying material that’s too advanced for them, then the studying is not going to be very effective. It’ll be like practicing a wheelie when they can barely ride a bike. Or practicing an ice skating spin when they can’t even glide straight on one leg.

The point that I’m trying to make with my post is this:

• If you're coming into an elite university, you're taking intense math classes, and you want to guard yourself against getting screwed over like that and falling through the cracks, then it would be a good idea to spin up on math beyond AP Calc BC.
• You probably won't hear anyone explicitly tell you you need to do that, but the way the courses are often run (maybe not in theory but often in practice), there will likely be an implicit assumption that you are already comfortable or at least familiar with a lot of that stuff.
• Why? Because lots of math instructors at elite universities, being of far outsized aptitude and often having far outsized mathematical upbringings, don't have a good frame of reference for what high school math covers is or how well non-genius students can identify and spin up on missing prerequisite knowledge.
• The content that many other math majors at elite universities are going to come in already knowing, beyond the standard high school curriculum and competition math, is linear algebra, multivar calc, and proof-writing including inklings of real analysis (e.g., epsilon-delta limit proofs) and abstract algebra (e.g., structure of the additive & multiplicative groups of integers). So if you want to be well-prepared, that's what you should aim to come in with too. In particular, get really solid on proof-writing, because that's where the lion's share of missing prerequisite knowledge is going to be.

Q: This is happening to me right now 😭. Any advice?

A: It will be rough, but there is a way through, if you can identify the foundations that you’re missing, identify quality resources to help you fill them in, and you have it in you to put forth however much work is needed to make that happen.

Q: Oh shit. My oldest daughter is going through this. What to do?

A: A good tutor can save the day. I don’t tutor anymore but a couple years ago I tutored a family member who was going through it. I’ll tell you more about the context and what we did to resolve the situation.

The instructor was terrible, HW was never graded (completion only), there was no textbook and no instructor notes. Only graded work was midterm, which was not returned until week before final.

HW exercises were typically given at the most abstract level possible (whereas you really need to scaffold up to them with a series of concrete examples starting with the simplest case possible and gradually increasing in difficulty/generality).

I’m told the instructor’s class engagement was limited to “anyone have any questions about the theorem/proof that I wrote down? (silence) No? Alright, I’m going to write down the next theorem/proof.”

So I stepped in to save the day. I’ll paste a snippet from this post where I talked about what we did in our tutoring sessions:

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.