Effective Learning Requires Intense Effort

by Justin Skycak (@justinskycak) on January 11, 2024

Effortful processes like testing, repetition, and computation are essential parts of effective learning, and competition is often helpful.

This post is part of the book The Math Academy Way (Working Draft, Jan 2024). Suggested citation: Skycak, J., advised by Roberts, J. (2024). Effective Learning Requires Intense Effort. In The Math Academy Way (Working Draft, Jan 2024). https://justinmath.com/effective-learning-requires-intense-effort/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

Is there any form of effective practice that requires low or no effort?

Absolutely not. Talent development takes work – not just a little work, but a lot of work. There is absolutely no confusion about this in the talent development community. Can you imagine asking an athletic coach to help you become a star player using training methods that don’t tire you out and make you sweat?

A common theme in the science of learning is that effective learning feels like a workout with a personal trainer. It should center around deliberate practice, a type of active learning in which individualized training activities are specially chosen to improve specific aspects of performance through repetition and successive refinement. These practice activities are done entirely for the purpose of pushing one’s limits and improving performance; consequently, they tend to be more effortful and less enjoyable.

Unfortunately, many types of training methods are ineffective, but require little effort, and can therefore seem attractive to even the most well-intentioned, hardworking students because they create an illusion of competence (e.g. Karpicke, Butler, & Roediger, 2009; also called an illusion of comprehension in earlier works reviewed in e.g. Bjork & Bjork, 2023). Examples include looking at notes, rereading course materials, and highlighting. In a review of scientific studies on various methods of practice, low-effort methods like these were found to have the lowest utility in terms of promoting learning, retention, and application of knowledge (Dunlosky et al., 2013):

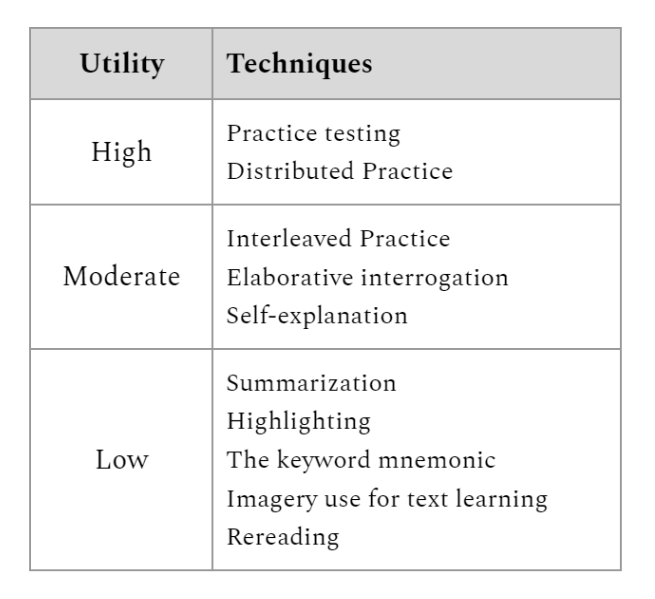
On the other hand, the two highest-utility methods – practice testing and distributed practice – are particularly effortful. The benefits of practice testing come from effortful retrieval of information, and the benefits of distributed practice come from spreading out practice sessions to allow for some amount of forgetting to set in between them (which thereby increases the level of effort required during subsequent practice sessions). As Brown, Roediger, & McDaniel (2014, pp.48) summarize:

"Spacing out your practice feels less productive for the very reason that some forgetting has set in and you've got to work harder to recall the concepts. It doesn't feel like you're on top of it. What you don't sense in the moment is that this added effort is making the learning stronger."

And as Kang (2016) describes, these two high-effort methods are even more effective (and, of course, even more effortful) when combined:

"Testing or spaced practice, each on its own, confers considerable advantages for learning. But, even better, the two strategies can be combined to amplify the benefits: Reviewing previously studied material can be accomplished through testing (often followed by corrective feedback) instead of rereading."

To be clear, this is not to say that passively reading or re-reading material should be completely avoided. It is useful to familiarize oneself with instructional material before engaging in effortful practice, and it is also useful to revisit that material if one runs into issues while attempting to carry out the effortful practice. However, it is not until effortful practice that true learning actually occurs.

Familiarizing oneself with instructional material is similar to warming up before a workout: the warmup does not actually lead to improvements in strength or endurance, but it does help maximize performance and avoid injury during the workout. No matter what skill is being trained, improving performance is always an effortful process.

As Qadir & Imran (2018) summarize, learning is all about creating desirable difficulties:

"While we intuitively dislike difficulties and thus try to avoid them, many difficulties (but not all) have a positive effect on learning. The well-known cognitive psychologist Bob Bjork coined the term 'desirable difficulties' for such difficulties that have a positive effect on learning.
...
Learning -- i.e., actual learning that requires the ability to remember and transfer concepts in the long term -- requires effort ... Research has shown that while retrieval is harder with spaced learning and interleaving, resulting in the feeling that the learning is less accomplished, the resulting learning is actually deeper and will lead to easier retrieval in the future."

To Oppose Effortful Practice is to Oppose Talent Development

A closely related myth is that testing, repetition, computation, and competition detract from learning.

But the reality is that in the world of talent development, nobody is confused about the importance of these methods. Can you imagine telling an athletic coach that things like competitive tryouts, repetitious drills, exhausting physical conditioning, and assigning playing time based on performance during scrimmage and competitive games against other teams, detract from developing athletic talent?

Testing and Repetition are Necessary

As discussed earlier in this post, practice testing and distributed practice (also known as spaced repetition) are widely understood by researchers to be two of the most effective practice techniques. Previous posts have also discussed the importance of deliberate practice, individualized training activities specially chosen to improve specific aspects of a student’s performance through repetition and successive refinement, which has been shown to be one of the most prominent underlying factors responsible for individual differences in performance, even among highly talented elite performers.

It is not possible to rationally argue that one can maximize learning without engaging in testing and repetition. If someone attempts to argue that position, what they are really saying is that they disagree with the premise of maximizing learning. And that is fine – plenty of people would prefer for their education to maximize other things like fun and entertainment while, as a secondary concern, meeting some low bar for shallowly learning some surface-level basic skills. But that is a completely different and opposite thing from talent development.

What’s more, in a subject as hierarchical as math, where each advanced skill requires many simpler skills to be applied in complex ways, avoiding testing and repetition can lead to major struggle. To learn a complex skill, a student must first be fluent with the simpler component skills – and to comfortably perform the complex skill, a student must be fully automatic with the simpler component skills. If a student does not develop fluency and eventual automaticity on each skill, they will be doomed to struggle on the more advanced skills of which those simpler skills are components. Testing and repetition are the two learning strategies that most directly build fluency and eventual automaticity. (To be clear, repetition does not mean giving students excessive practice past the point of mastery, but rather, giving students enough practice to achieve mastery before moving them on to more advanced skills.)

Computation is Necessary

There are several reasons why practicing computation is a necessary part of learning math.

In the absence of computation, it's easy to lose touch with the concrete meaning of various symbols, procedures, and ideas. Computation keeps learners aware of what these things mean in terms of concrete numbers. In fact, the whole point of an abstract idea is to streamline and unify existing knowledge of concrete examples. Computational examples are to mathematics as experiences are to life.
Is someone a talented basketball player if they can talk about the strategy of the game but cannot actually make any shots? No. The same applies to someone who can talk about mathematical ideas but is unable to perform computations.
It is impossible to gain a full, holistic understanding of a subject without knowing the component skills. If someone can't shoot a basketball, how can they possibly understand how different shots compare in terms of difficulty, and what plays might open up good shots? The same is true in mathematics.
Computation often helps build conceptual understanding. Math is full of ideas that cannot be properly understood without experience carrying out computations. (One of the clearest examples of this is the concept of the discriminant of a quadratic equation: if a student has experience computing solutions to quadratic equations using the quadratic formula, then they will find it much easier to observe that the $b^2-4ac$ term, known as the discriminant, controls the number of solutions.)

Math resources that don’t give proper emphasis to computation end up having to water down their curriculum and cherry-pick problems, giving students the easiest possible problem-solving cases that don’t require too much in the way of foundational skills. That can be exciting for students because they get enough conceptual understanding to feel like they have learned the material in proper depth even though they actually haven’t.

This is fine if a student is just curious about math and wants to learn a bit without putting in too much time and effort – but if a student is serious about learning math well enough to make a career out of it, then watered-down courses won’t give them what they need. That’s where Math Academy comes in: we teach math as if we were training a professional athlete or musician, or anyone looking to acquire a skill to the highest degree possible, and we’ve designed the curriculum to go toe-to-toe against any similar course you would find in the top universities and the most popular textbooks in the world.

Silly Mistakes

Opponents of computation will sometimes claim that it unnecessarily slows down the learning process when students are given further practice in response to silly mistakes. However, in the context of a skill hierarchy like mathematics, it’s not good enough to be “almost” able to execute a skill properly. If a gymnast is “almost” able to land a backflip, then that’s great progress, but at the same time, they’re not ready to try any combination moves of which a backflip is a component. Even if it’s a silly mistake keeping the gymnast from landing the backflip, they still have to rectify it before layering on more advanced skills.

More generally, when students are not made to clean up their silly mistakes on low-level skills, they eventually hit a wall where no matter how hard they try, they are unable to reliably perform advanced skills due to the compounding probability of silly mistakes in the component skills.

Additionally, many students frequently claim that they made a silly mistake when in fact their mistake was indicative of a deeper conceptual misunderstanding. Sometimes this claim is in good faith (i.e., they honestly believe they made a silly mistake), other times it’s in bad faith (i.e., they’re trying to exploit the grading system to get credit they don’t deserve), but regardless, it’s something that needs to prevented.

Competition Can be Helpful and is Unavoidable in the Big Picture

While competition is not inherent to the learning process, appropriately structured competition does not necessarily detract from it either, and in many cases, can incentivize learners to increase the quantity and quality of practice to maximize their level of achievement.

Of course, this is not to say that every student must compete in order to learn productively. Similarly, this is not to say every form of competition promotes learning. The key phrase is appropriately structured competition. It is easy to imagine disaster scenarios arising from inappropriately structured competition (e.g. the student with the highest score gets an A and all others fail the class).

That said, if a student is serious about developing their talent to a high enough level to build a career around it, then competition is a reality that they must eventually face. In talent development, anyone who seriously attempts to reach any level of success in a sport, instrument, etc, knows that they have to work really hard and compete against other people (who are also working really hard) for limited positions. Mathematics is no exception. There is a limited number of professorships available for mathematics and related disciplines, and outside academia, there is a limited number of positions available for jobs that involve solving hard problems using advanced mathematics.

It’s worth emphasizing that while competition gets a bad rap, its purpose is positive: generally speaking, the purpose of competition is to assign responsibilities to the people most capable of performing them and motivate those people to continue working hard and improving. The bad rap tends to be vocalized by people who are not aligned with this process – for instance, people who confuse their enjoyment of a job with their capability or value to society in performing it, or people who wait until the last minute to begin developing a talent and then experience a rude awakening when they realize that their level of capability is far behind that of other people.

Why the Myth Persists in Education (But Not in Talent Development)

Why does this myth persist in the practice of education, whereas there is no confusion in the field of talent development? One key factor is that in talent development, the optimization problem is clear: an individual’s performance is to be maximized, so the methods used during practice are those that most efficiently convert effort into performance improvements. On the other hand, in education, there are many other factors (especially bureaucratic ones) that constrain and cloud the optimization problem. The end result is that teachers are incentivized to use easy, fun, low-accountability, hard-to-measure practice techniques that keep students, parents, and administrators off their back. Unfortunately, these practice techniques tend to be ineffective.

For instance, consider the idea of testing. In talent development, all parties involved are proponents of testing. If a child is training to play a sport at a high level, such as becoming an Olympic sprinter, then the child, their parents, and their coach will all want to see regular measurements of the child’s 100-meter dash time. If that time is going down, then practice is working and everybody is happy. If the time is not going down, then it signals that something needs to be adjusted in the practice routine and nobody is happy until the problem is solved. The act of measuring performance is critical because it tells everyone whether the child is making progress towards achieving their goal.

In education, however, many people are against testing. Typically, parents want their children to get high grades and learn a bit without feeling too stressed, their children want to minimize the amount of work they have to do to satisfy (or, perhaps, not anger) their parents, and administrators want parents to be happy and test scores to be sufficiently high. Teachers are squeezed by pressure on both sides – getting as many kids as possible over some threshold test score, while assigning as high grades and as little work as possible.

In this position, it is easy to dislike testing – if testing were to go away, then it would be easy to satisfy all parties involved by centering the class around discussions and fun activities. Students wouldn’t have to work too hard, they would learn a little bit, they would receive good grades on the basis of participation, parents would be happy that their children are getting high grades and learning a bit without feeling too stressed, and administrators would be happy that parents are happy. It is only natural for those in this position to oppose testing and instead argue for the existence and importance of subjective forms of learning that cannot be objectively measured, even though such forms of learning are unscientific by definition.

Why Talent Development is Important in Math

Practitioners of talent development tend to be found in hierarchical skill domains like sports and music, where each advanced skill requires many simpler skills to be applied in complex ways. This is because it’s hard to climb up the skill hierarchy without intentionally trying to do so.

To learn an advanced skill, you must be able to comfortably execute its prerequisite skills, and the prerequisite skills underlying those, and so on. Getting to the point of comfortable execution on any skill takes lots of practice over time – and even after you get there, you have to continue practicing to maintain your ability.

None of this happens naturally. If you don’t carefully manage the process, then you struggle. Nobody gets to be really good at a sport or instrument without taking their talent development seriously and intentionally trying to maximize their learning.

Conveniently, most students aren’t expected to achieve a high level of success in sports or music, so they can get away with de-prioritizing talent development. If every student in gym class were expected to be able to do a backflip by the end of the year, things would have to change – but the expectations are so low that meeting them does not require talent development.

When it comes to math, however, things become problematic. Like sports and music, math is an extremely hierarchical skill domain, so achieving a high level of success requires a dedication to talent development. However, unlike sports and music, most students are expected to achieve a relatively high level of success in math: many years of courses increasing in difficulty, culminating in at least algebra, typically pre-calculus, often calculus, and sometimes even higher than that.

As a result, in math, de-prioritizing talent development leads to major issues. When students do the mathematical equivalent of playing kickball during class, and then are expected to do the mathematical equivalent of a backflip at the end of the year, it’s easy to see how struggle and general negative feelings can arise.

References

Bjork, E. L., & Bjork, R. A. (2023). Introducing Desirable Difficulties Into Practice and Instruction: Obstacles and Opportunities. In C. Overson, C. M. Hakala, L. L. Kordonowy, & V. A. Benassi (Eds.), In Their Own Words: What Scholars and Teachers Want You to Know About Why and How to Apply the Science of Learning in Your Academic Setting (pp. 111-21). Society for the Teaching of Psychology.

Brown, P. C., Roediger III, H. L., & McDaniel, M. A. (2014). Make it stick: The science of successful learning. Harvard University Press.

Dunlosky, J., Rawson, K. A., Marsh, E. J., Nathan, M. J., & Willingham, D. T. (2013). Improving students’ learning with effective learning techniques: Promising directions from cognitive and educational psychology. Psychological Science in the Public interest, 14(1), 4-58.

Kang, S. H. (2016). Spaced repetition promotes efficient and effective learning: Policy implications for instruction. Policy Insights from the Behavioral and Brain Sciences, 3(1), 12-19.

Karpicke, J. D., Butler, A. C., & Roediger III, H. L. (2009). Metacognitive strategies in student learning: Do students practise retrieval when they study on their own?. Memory, 17(4), 471-479.

Qadir, J., & Imran, M. A. (2018). Learning 101: The untaught basics. IEEE Potentials, 37(3), 33-38.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.