Dot Product and Cross Product

by Justin Skycak (x.com/justinskycak) on June 02, 2019

What does it mean to multiply a vector by another vector?

This post is part of the book Justin Math: Linear Algebra. Suggested citation: Skycak, J. (2019). Dot Product and Cross Product. In Justin Math: Linear Algebra. https://justinmath.com/dot-product-and-cross-product/

Want to get notified about new posts? Join the mailing list.

We know how to multiply a vector by a scalar, but what does it mean to multiply a vector by another vector?

The two most common interpretations of vector multiplication are the dot product, and for vectors in 3 dimensions, the cross product.

Dot Product

The dot product is computed as the sum of products of components.

$\begin{align*} \left< x_1, x_2, \ldots, x_n \right> \cdot \left< y_1, y_2, \ldots, y_n \right> = x_1y_1 + x_2y_2 + \ldots + x_ny_n \end{align*}$

First of all, notice that the dot product of a vector with itself is just the vector’s norm, squared.

$\begin{align*} &\left< x_1, x_2, \ldots, x_n \right> \cdot \left< x_1, x_2, \ldots, x_n \right> \\ &= x_1^2+x_2^2 + \ldots + x_n^2 \\ &= \left( \sqrt{x_1^2+x_2^2 + \ldots + x_n^2} \right)^2 \\ &= \left| \left< x_1, x_2, \ldots, x_n \right> \right|^2 \end{align*}$

Also notice that the dot product can distribute over sums of vectors, just like multiplication.

$\begin{align*} &\left< x_1, x_2, \ldots, x_n \right> \cdot \left( \left< y_1,y_2, \ldots, y_n \right> + \left< z_1, z_2, \ldots, z_n \right> \right) \\ &= \left< x_1, x_2, \ldots, x_n \right> \cdot \left( \left< y_1+z_1 ,y_2+z_2 , \ldots, y_n+z_n \right> \right) \\ &= x_1(y_1+z_1) +x_2(y_2+z_2) + \ldots +x_n(y_n+z_n) \\ &= x_1y_1+x_1z_1 +x_2y_2+x_2z_2 + \ldots +x_ny_n+x_nz_n \\ &= \left( x_1y_1+x_2y_2+\ldots+x_ny_n\right) + \left( x_1z_1+x_2z_2+\ldots+x_nz_n \right) \\ &= \left< x_1, x_2, \ldots, x_n \right> \cdot \left< y_1, y_2, \ldots, y_n \right> + \left< x_1, x_2, \ldots, x_n \right> \cdot \left< z_1, z_2, \ldots, z_n \right> \end{align*}$

One can also verify that the dot product behaves like multiplication in other ways – for example for two vectors $x=\left< x_1, x_2, \ldots, x_n \right>$ and $y=\left< y_1, y_2, \ldots, y_n \right>$ and any scalar $c$ we have $(cx) \cdot y = x \cdot (cy) = c(x \cdot y)$ and $x \cdot y = y \cdot x$.

Geometric Interpretation of Dot Product

Using the law of cosines on a triangle whose sides are formed by the vectors $x$, $y$, and $x-y$, we can find a geometric interpretation of the dot product:

$\begin{align*} x \cdot y = \|x\| \|y\| \cos \theta, \end{align*}$

where $\theta$ is the angle between the two vectors $x$ and $y$.

$\begin{align*} |x-y|^2 &= |x|^2+|y|^2-2|x||y| \cos \theta \\ (x-y) \cdot (x-y) &= |x|^2+|y|^2-2|x||y| \cos \theta \\ x \cdot x - x \cdot y - y \cdot x + y \cdot y &= |x|^2+|y|^2-2|x||y| \cos \theta \\ |x|^2-2x \cdot y + |y|^2 &= |x|^2+|y|^2-2|x||y| \cos \theta \\ -2x \cdot y &= -2|x||y| \cos \theta \\ x \cdot y &= |x| |y| \cos \theta \end{align*}$

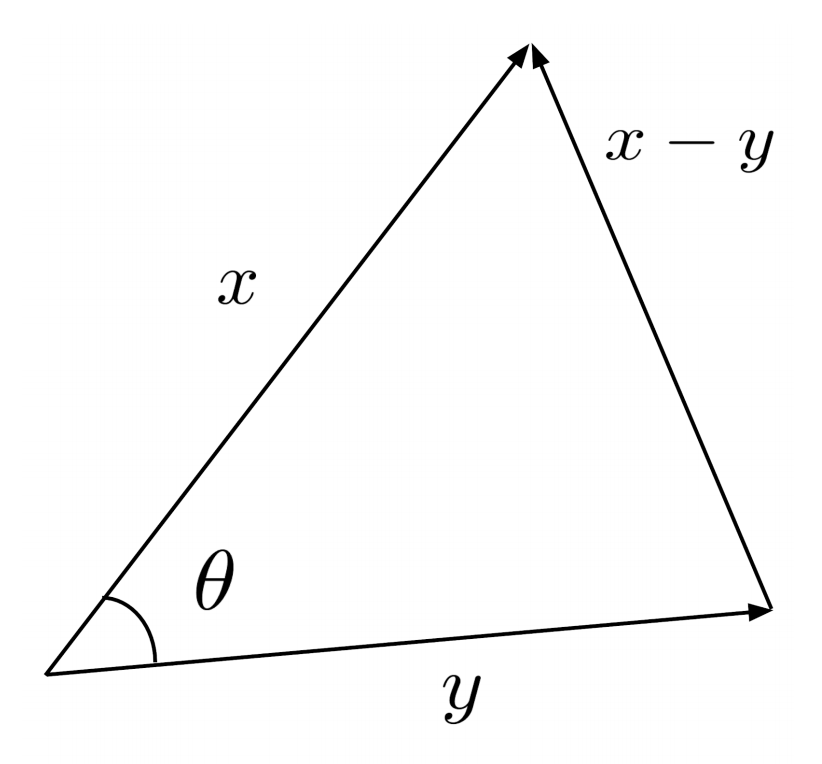
One interesting consequence of this formula is that perpendicular vectors have a dot product of zero: the angle between perpendicular vectors $\frac{\pi}{2}$ is $|x| |y| \cos \frac{\pi}{2} = |x| |y| (0) = 0$.

Even if the dot product is not zero, we can still use it to compute the angle between the two vectors.

$\begin{align*} x \cdot y &= |x| |y| \cos \theta \\ \frac{x \cdot y}{|x| |y|} &= \cos \theta \\ \arccos \left( \frac{x \cdot y}{|x| |y|} \right) &= \theta \end{align*}$

Cross Product

For 3-dimensional vectors, we also have another interpretation of vector multiplication called the cross product. The cross product is given by

$\begin{align*} &\left< x_1, x_2, x_3 \right> \times \left< y_1, y_2, y_3 \right> \\ &= \left< x_2y_3-x_3y_2, x_3y_1-x_1y_3, x_1y_2-x_2y_1 \right>. \end{align*}$

Using the above definition, one can verify that the cross product distributes over sums and satisfies $(cx) \times y = x \times (cy) = c(x \times y)$ for any scalar $c$.

However, when the two vectors in a cross product are interchanged, the result changes sign: $x \times y = -y \times x$. This is a key difference between the cross product and the dot product.

Geometric Interpretation of Cross Product

Like the dot product, the cross product also has a geometric interpretation:

$\begin{align*} \| x \times y \| = \|x\| \|y\| \sin \theta \end{align*}$

This is similar to the geometric interpretation of the dot product, except we have $\sin \theta$ instead of $\cos \theta$, and we are talking about the norm of the vector resulting from the cross product.

As a result, the cross product $x \times y$ represents a vector whose norm is equal to the area enclosed by the parallelogram that has $x$ and $y$ as sides. Moreover, the cross product produces a vector that is perpendicular to the vectors $x$ and $y$.

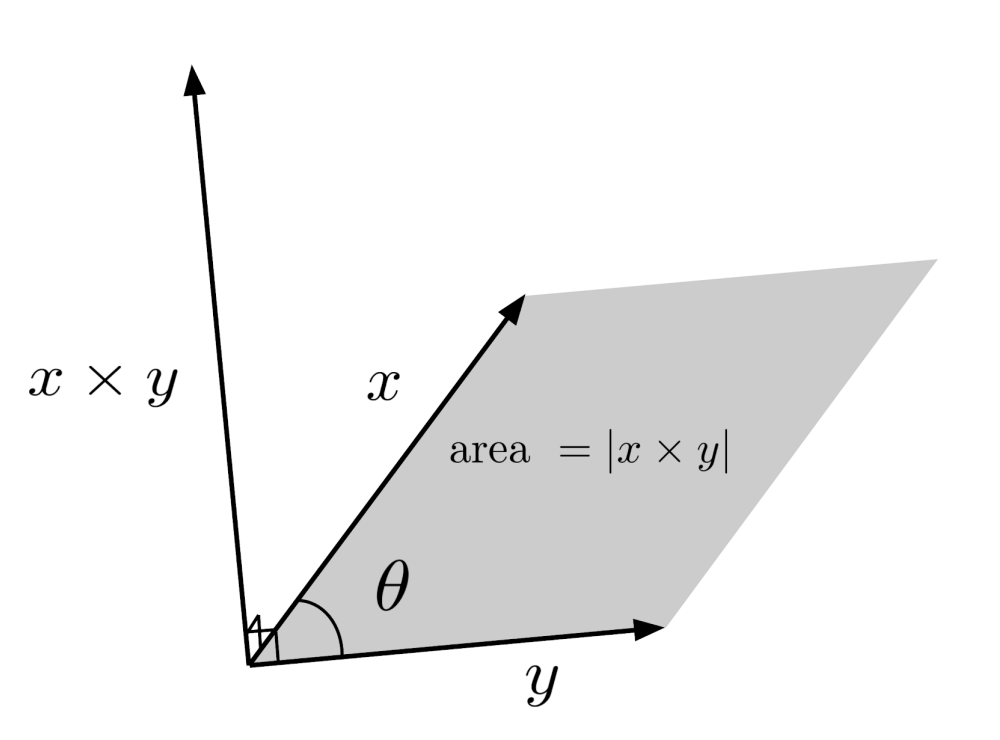
To see that the cross product $x \times y$ is perpendicular to $x$ and $y$, observe that the dot products $(x \times y) \cdot x$ and $(x \times y) \cdot y$ both evaluate to $0$.

$\begin{align*} &\left( \left< x_1, x_2, x_3 \right> \times \left< y_1, y_2, y_3 \right> \right) \cdot \left< x_1, x_2, x_3 \right> \\ &= \left< x_2y_3-x_3y_2, x_3y_1-x_1y_3, x_1y_2-x_2y_1 \right> \cdot \left< x_1, x_2, x_3 \right> \\ &= x_1(x_2y_3-x_3y_2)+x_2( x_3y_1-x_1y_3)+x_3( x_1y_2-x_2y_1) \\ &= x_1x_2y_3 - x_1x_3y_2 + x_2x_3y_1-x_1x_2y_3 + x_1x_3y_2-x_2x_3y_1 \\ &= 0 \end{align*}$

$\begin{align*} &\left( \left< x_1, x_2, x_3 \right> \times \left< y_1, y_2, y_3 \right> \right) \cdot \left< y_1, y_2, y_3 \right> \\ &= \left< x_2y_3-x_3y_2, x_3y_1-x_1y_3, x_1y_2-x_2y_1 \right> \cdot \left< y_1, y_2, y_3 \right> \\ &= y_1(x_2y_3-x_3y_2)+y_2( x_3y_1-x_1y_3)+y_3( x_1y_2-x_2y_1) \\ &= x_2y_1y_3-x_3y_1y_2+x_3y_1y_2-x_1y_2y_3+x_1y_2y_3-x_2y_1y_3 \\ &= 0 \end{align*}$

To understand why $| x \times y | = |x| |y| \sin \theta$, we can begin by squaring both sides of the equation and expressing the right-hand side using the dot product.

$\begin{align*} \left| x \times y \right|^2 &= \left| x \right|^2 \left| y \right|^2 \sin^2 \theta \\ &= \left| x \right|^2 \left| y \right|^2 \left( 1-\cos^2 \theta \right) \\ &= \left| x \right|^2 \left| y \right|^2 - \left| x \right|^2 \left| y \right|^2 \cos^2 \theta \\ &= \left| x \right|^2 \left| y \right|^2 - (x \cdot y)^2 \end{align*}$

Now, we expand out the right hand side using $x = \left< x_1, x_2, x_3 \right>$ and $y = \left< y_1, y_2, y_3 \right>$. We find that some terms cancel, and the remaining terms can be rearranged into the square of the norm of the cross product.

$\begin{align*} &\left( x_1^2 + x_2^2 + x_3^2 \right) \left( y_1^2 + y_2^2 + y_3^2 \right) - \left( x_1y_1 + x_2y_2 + x_3y_3 \right)^2 \\ &= \begin{pmatrix} x_1^2y_1^2 + x_1^2y_2^2 + x_1^2y_3^2 \\ x_2^2y_1^2 + x_2^2y_2^2 + x_2^2y_3^2 \\ x_3^2y_1^2 + x_3^2y_2^2 + x_3^2y_3^2 \end{pmatrix} - \begin{pmatrix} x_1^2y_1^2 + x_1x_2y_1y_2 + x_1x_3y_1y_3 \\ + x_1x_2y_1y_2 + x_2^2y_2^2 + x_2x_3y_2y_3 \\ + x_1x_3y_1y_3 + x_2x_3y_2y_3 + x_3^2y_3^2 \end{pmatrix} \\ &= x_2^2y_3^2 + x_3^2y_2^2 - 2x_2x_3y_2y_3 + x_3^2y_1^2 + x_1^2y_3^2 - 2x_1x_3y_1y_3 \\ & \hspace{.5cm} + x_1^2y_2^2 + x_2^2y_1^2 - 2x_1x_2y_1y_2 \\ &= \left( x_2y_3 - x_3y_2 \right)^2 + \left( x_3y_1 - x_1y_3 \right)^2 + \left( x_1y_2 - x_2y_1 \right)^2 \\ &= \left| \left< x \times y \right> \right|^2 \end{align*}$

Exercises

Evaluate the following vector expressions. (You can view the solution by clicking on the problem.)

$1) \hspace{.5cm} \left< 1,2,4 \right> \cdot \left< -1,-2,3 \right>$

Solution:
$ 7 $

$2) \hspace{.5cm} \left< 2,-2,3,3 \right> \cdot \left< -1,1,1,-1 \right> $

Solution:
$ -4 $

$3) \hspace{.5cm} 2 \left< 2,3 \right> \cdot \frac{1}{2} \left< 3,-2 \right> $

Solution:
$ 0 $

$4) \hspace{.5cm} \frac{1}{2} \left< 1,4,-2 \right> \cdot ( \left< 3,3,1 \right> - \left< 1,3,3 \right> ) $

Solution:
$ 3 $

$5) \hspace{.5cm} \left< -2,1,0 \right> \times \left< -2,3,0 \right> $

Solution:
$ \left< 0,0,-4 \right> $

$6) \hspace{.5cm} \left< 3,1,5 \right> \times \left< 2,-2,-1 \right> $

Solution:
$ \left< 9,13,-8 \right> $

$7) \hspace{.5cm} \left< 1,1,2 \right> \times (\left< 2,4,6 \right> - \left< 1,4,7 \right>) $

Solution:
$ \left< -1,3,-1 \right> $

$8) \hspace{.5cm} \frac{1}{3} \left< 1,0,2 \right> \times \left< 1,1,1 \right> \times \left< 0,0,3 \right> $

Solution:
$ \left< 1,2,0 \right> $

Solve for $x$. (You can view the solution by clicking on the problem.)

$9) \hspace{.5cm} \left< x,1,2 \right> \cdot \left< 1,2,x \right> = -4 $

Solution:
$x= -2 $

$10) \hspace{.5cm} \left< x,1 \right> \cdot (\left< 1,1 \right> - \left< 1,x \right> )=1 $

Solution:
$x= 0 $

$11) \hspace{.5cm} \left< x,-1,0,1 \right> \times \left< x,0,5,7 \right> = 16 $

Solution:
$x= \pm 3 $

$12) \hspace{.5cm} \left< 1,2,3 \right> \times \left< 1,x,3 \right> = \left< -6,0,2 \right> $

Solution:
$x= 4 $

$13) \hspace{.5cm} \left< 1,1,1 \right> \times (\left< 2,1,-2 \right> + \left< x,1,1 \right> ) = \left< -3,2,1 \right> $

Solution:
$x= -1 $

$14) \hspace{.5cm} \frac{1}{2} \left< 3,1,-2 \right> \times (\left< 0,x,0 \right> - \left< 1,0,2 \right> ) = \left< 2,4,5 \right> $

Solution:
$x= 3 $

Use the dot product to find the angle $\theta$ between the two vectors. (You can view the solution by clicking on the problem.)

$\begin{align*} 15) \hspace{.5cm} &\left< 1,1 \right> \\ & \left< 1,2 \right> \end{align*}$

Solution:
$\begin{align*} &\arccos \left( \frac{3}{ \sqrt{10} } \\ &\approx 18.43^\circ \end{align*}$

$\begin{align*} 16) \hspace{.5cm} &\left< -2,3,1\right> \\ & \left< 0,1,-1 \right> \end{align*}$

Solution:
$\begin{align*} &\arccos \left( \frac{1}{ \sqrt{7} } \\ &\approx 67.79^\circ \end{align*}$

$\begin{align*} 17) \hspace{.5cm} &\left< 2,0,3,-1 \right> \\ & \left< 1,1,0,2 \right> \end{align*}$

Solution:
$\frac{\pi}{2} = 90^\circ$

$\begin{align*} 18) \hspace{.5cm} &\left< 2,0,-1,0,2 \right> \\ & \left< -1,2,3,0,0 \right> \end{align*}$

Solution:
$\begin{align*} &\arccos \left(- \frac{5}{ 3\sqrt{14} } \\ &\approx 116.45^\circ \end{align*}$

Use the cross product to find the area contained by each parallelogram whose sides are given as vectors.

$\begin{align*} 19) \hspace{.5cm} &\left< 2,-1,0 \right> \\ & \left< 4,1,0 \right> \end{align*}$

Solution:
$ 6 $

$\begin{align*} 20) \hspace{.5cm} &\left< 1,2,3 \right> \\ & \left< 3,2,1 \right> \end{align*}$

Solution:
$ 4\sqrt{6} $

$\begin{align*} 21) \hspace{.5cm} &\left< 1,0,1 \right> \\ & \left< 1,1,1 \right> \end{align*}$

Solution:
$ \sqrt{2} $

$\begin{align*} 22) \hspace{.5cm} &\left< 3,-3,1 \right> \\ & \left< -4,1,-2 \right> \end{align*}$

Solution:
$ \sqrt{110} $

Want to get notified about new posts? Join the mailing list.