Differentials and Approximation

by Justin Skycak (@justinskycak) on January 09, 2019

We can interpret the derivative as an approximation for how a function's output changes, when the function input is changed by a small amount.

This post is part of the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). Differentials and Approximation. In Justin Math: Calculus. https://justinmath.com/differentials-and-approximation/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

The chain rule tells us that we can treat the derivative $\frac{df}{dx}$ like a fraction when multiplying by other derivatives. In this chapter, we continue the idea of interpreting the derivative as a fraction, extending it to an even more literal sense.

The main idea of differentials is that we can interpret the derivative $\frac{df}{dx}$ as an approximation for how the function output changes, when the function input is changed by a small amount. The terms $df$ and $dx$ are called differentials, and we can interpret them as small changes in the function’s output and input.

Demonstration

For example, if we know that $f(4)=2$ and $f’(4)=5$ for some function $f(x)$, then we can estimate the value of $f(4.1)$ by treating the differentials as small changes in $x$ and $f(x)$.

$\begin{align*} \frac{df}{dx} \bigg|_{x=4} &= 5 \\ \frac{\Delta f}{\Delta x}\bigg|_{x=4} &\approx 5 \\ \frac{f(4.1)-f(4)}{4.1-4} &\approx 5 \\ \frac{f(4.1)-2}{0.1} &\approx 5 \\ f(4.1)-2 &\approx 0.5 \\ f(4.1) &\approx 2.5 \end{align*}$

We can use this method to estimate values of functions that are difficult to compute, like trig functions and roots.

For example, we know that $\sin 0 = 0$ and that $(\sin x)’\big\vert_{x=0} = \cos 0 = 1$, so we can estimate the value of using differentials.

$\begin{align*} \frac{d (\sin x)}{dx} \bigg|_{x=0} &\approx \frac{\Delta (\sin x)}{\Delta x}\bigg|_{x=0} \\ \cos 0 &\approx \frac{\sin 0.1 - \sin 0}{0.1 - 0} \\ 1 &\approx \frac{\sin 0.1 - 0}{0.1} \\ 0.1 &\approx \sin 0.1 \end{align*}$

Our estimation is pretty good – the actual value of $\sin 0.1$ is $0.099833\ldots$

Similarly, we know that $\sqrt{144}=12$ and that $\left( \sqrt{x} \right)’ \big|_{x=144} = \frac{1}{2\sqrt{144}} = \frac{1}{24}$, so we can estimate the value of $\sqrt{149}$ using differentials.

$\begin{align*} \frac{d (\sqrt{x})}{dx} \bigg|_{x=144} &\approx \frac{\Delta (\sqrt{x})}{\Delta x}\bigg|_{x=144} \\ \frac{1}{2\sqrt{144}} &\approx \frac{\sqrt{149} - \sqrt{144}}{149 - 144} \\ \frac{1}{24} &\approx \frac{\sqrt{149}-12}{5} \\ \frac{5}{24} &\approx \sqrt{147}-12 \\ 12 \frac{5}{24} &\approx \sqrt{147} \\ 12.208 &\approx \sqrt{147} \end{align*}$

Again, our estimation is pretty good – the actual value of $\sqrt{147}$ is $12.206555 \ldots$

Intuition

To understand why we can interpret the differentials as small changes, remember that the difference quotient is a good approximation for the derivative, when the difference $\Delta x$ is small.

$\begin{align*} \frac{df}{dx} &= \lim\limits_{\Delta x \to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} \\ &\approx \frac{f(x+\Delta x)-f(x)}{\Delta x} \end{align*}$

The numerator is really just the change in the values of the function $f$, so we can represent it by $\Delta f = f(x+\Delta x)-f(x)$.

$\begin{align*} \frac{df}{dx} &\approx \frac{\Delta f}{\Delta x} \end{align*}$

Graphically, approximating via differentials amounts to approximating with a tangent line. We start at the point $(x,f(x))$, travel $\Delta x$ units horizontally, and find the y-value that allows us to maintain a slope of $f’(x)$.

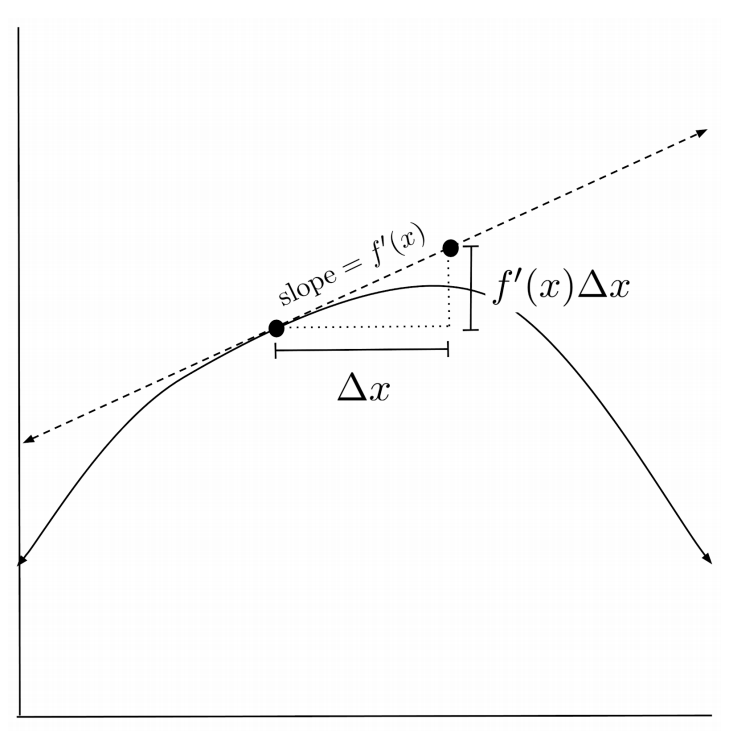
Since the tangent line goes through the point $(x,f(x))$ with slope $f’(x)$, the points $(X,Y)$ on the tangent line are given by the following linear equation in point-slope form:

$\begin{align*} Y - f(x) = f'(x)(X-x) \end{align*}$

Interpreting $X=x+\Delta x$ and $Y \approx f(x+\Delta x)$, we see that this equation is equivalent to the one we’ve been working with.

$\begin{align*} Y - f(x) &= f'(x)(X-x) \\ \frac{Y - f(x)}{X-x} &= f'(x) \\ \frac{Y - f(x)}{x+\Delta x-x} &= f'(x) \\ \frac{Y - f(x)}{\Delta x} &= f'(x) \\ \frac{f(x+\Delta x) - f(x)}{\Delta x} &\approx f'(x) \\ \frac{\Delta f}{\Delta x} &\approx f'(x) \end{align*}$

Exercises

Approximate each value by using differentials and the given equality. In your computations, use $\pi \approx 3.14$, $e \approx 2.72$, and $\sqrt{3} \approx 1.73$, and round to 2 decimal places. (You can view the solution by clicking on the problem.)

$\begin{align*}1) &\hspace{.5cm} (4.8)^2 \approx \underline{\hspace{.5cm}} \\ &\hspace{.5cm} 5^2 = 25 \end{align*}$

Solution:
$\begin{align*} 23.00 \end{align*}$

$\begin{align*} 2) &\hspace{.5cm} \sqrt{15} \approx \underline{\hspace{.5cm}} \\ &\hspace{.5cm} \sqrt{16} = 4 \end{align*}$

Solution:
$\begin{align*} 3.88 \end{align*}$

$\begin{align*}3) &\hspace{.5cm} \sqrt[3]{-7} \approx \underline{\hspace{.5cm}} \\ &\hspace{.5cm} \sqrt[3]{-8} = -2 \end{align*}$

Solution:
$\begin{align*} -1.92 \end{align*}$

$\begin{align*} 4) &\hspace{.5cm} \cos \left( \frac{7\pi}{30} \right) \approx \underline{\hspace{.5cm}} \\ &\hspace{.5cm} \cos \left( \frac{\pi}{3} \right) = \frac{1}{2} \end{align*}$

Solution:
$\begin{align*} 0.77 \end{align*}$

$\begin{align*}5) &\hspace{.5cm} \sin \left( \frac{11\pi}{30} \right) \approx \underline{\hspace{.5cm}} \\ &\hspace{.5cm} \sin \left( \frac{\pi}{3} \right) = \frac{\sqrt{3}}{2} \end{align*}$

Solution:
$\begin{align*} 0.92 \end{align*}$

$\begin{align*}6) &\hspace{.5cm} \tan \left( \frac{5\pi}{16} \right) \approx \underline{\hspace{.5cm}} \\ &\hspace{.5cm} \tan \left( \frac{\pi}{4} \right) = 1 \end{align*}$

Solution:
$\begin{align*} 1.39 \end{align*}$

$\begin{align*}7) &\hspace{.5cm} \ln 3 \approx \underline{\hspace{.5cm}} \\ &\hspace{.5cm} \ln 2.72 \approx 1 \end{align*}$

Solution:
$\begin{align*} 1.09 \end{align*}$

$\begin{align*}8) &\hspace{.5cm} e^{1.1} \approx \underline{\hspace{.5cm}} \\ &\hspace{.5cm} e^1 \approx 2.72 \end{align*}$

Solution:
$\begin{align*} 2.99 \end{align*}$

$\begin{align*}9) &\hspace{.5cm} \arcsin 0.47 \approx \underline{\hspace{.5cm}} \\ &\hspace{.5cm} \arcsin 0.5 = \frac{\pi}{6} \end{align*}$

Solution:
$\begin{align*} 0.49 \end{align*}$

$\begin{align*}10) &\hspace{.5cm} \arccos 0.54 \approx \underline{\hspace{.5cm}} \\ &\hspace{.5cm} \arccos 0.5 = \frac{\pi}{3} \end{align*}$

Solution:
$\begin{align*} 1.00 \end{align*}$

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.