Cognitive Science of Learning: Minimizing Cognitive Load

by Justin Skycak (@justinskycak) on February 14, 2024

Different students have different working memory capacities. When the cognitive load of a learning task exceeds a student's working memory capacity, the student experiences cognitive overload and is not able to complete the task.

This post is part of the book The Math Academy Way (Working Draft, Jan 2024). Suggested citation: Skycak, J., advised by Roberts, J. (2024). Cognitive Science of Learning: Minimizing Cognitive Load. In The Math Academy Way (Working Draft, Jan 2024). https://justinmath.com/cognitive-science-of-learning-minimizing-cognitive-load/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

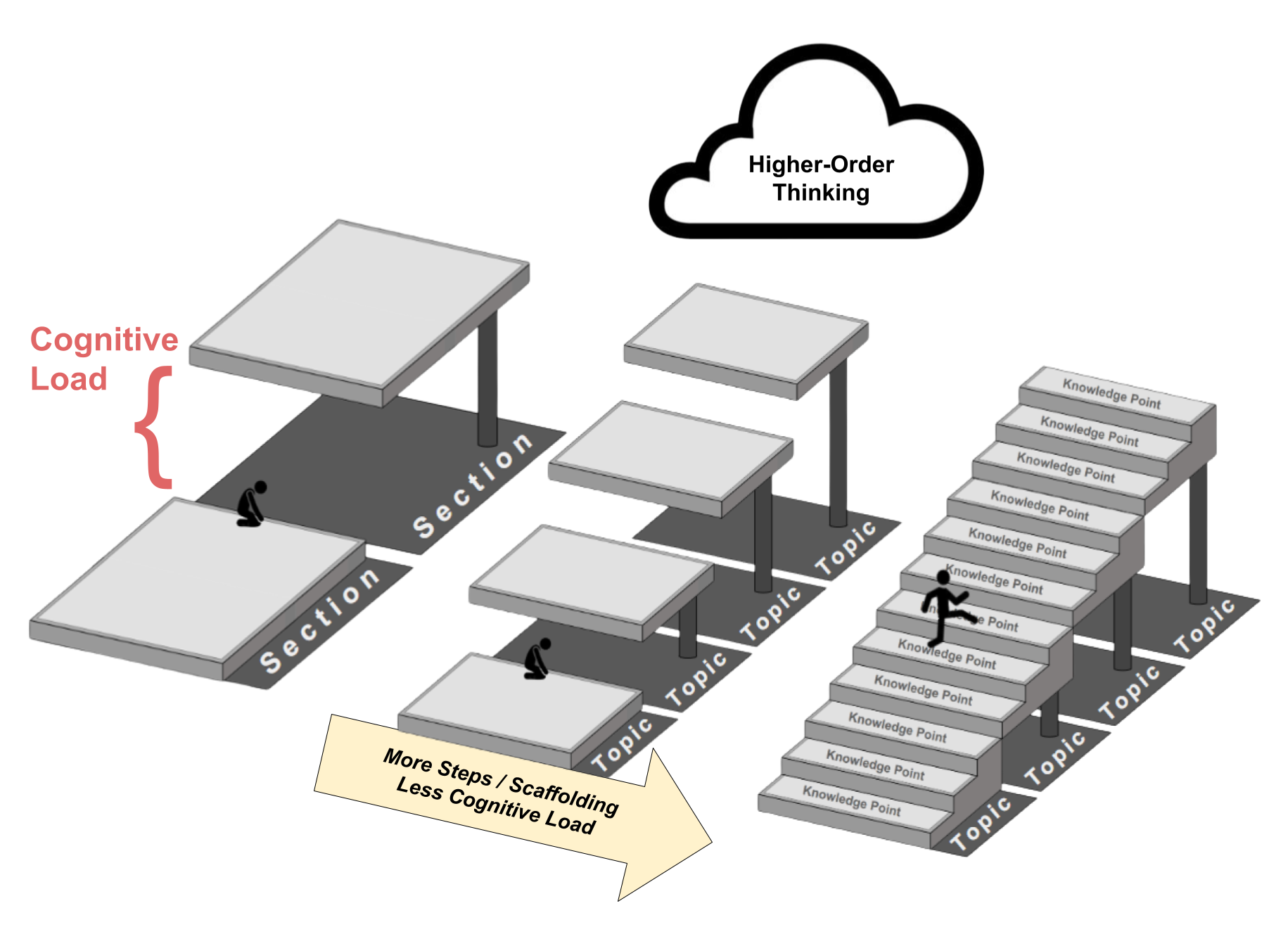
Learning is like climbing a staircase. Each step is a learning task – the higher the step, the more advanced the topic is. At the top of the staircase is higher-order thinking such as critical thinking and problem solving. However, different students have different stair-climbing abilities, and many students never make it to the top because they get stuck at individual stairs that are too tall for them to climb.

The solution is to split individual stairs into even smaller stairs so that all students can climb them. The smaller the individual stairs, the more students can climb all the way to the top.

Cognitive Overload

In technical terms, this amounts to minimizing cognitive load. Cognitive load refers to the amount of working memory that is required to complete a task. Working memory consists of limited-capacity, limited-duration short-term memory storage along with capabilities for organizing, manipulating, and generally “working” with the information stored in short-term memory.

In the staircase analogy, the height of each step represents cognitive load. Different students have different working memory capacities, and if the cognitive load of a learning task exceeds a student’s working memory capacity, then the student will not be able to complete the task due to cognitive overload.

Cognitive overload has massive negative ramifications for students: not only has working memory capacity been shown to predict performance in mathematical problem solving (Swanson & Beebe-Frankenberger, 2004), but perhaps shockingly, it has also been shown to be a better predictor than IQ when predicting a young student’s future academic success (Alloway & Alloway, 2010). By minimizing the cognitive load and avoiding cognitive overload, one can make learning accessible to many students for whom it would otherwise be insurmountable

Minimizing Cognitive Load

One of the most effective tools for minimizing cognitive load is worked examples. Worked examples have been show by numerous studies (see Sweller, 2006 for a review) to reduce cognitive load and help students develop a baseline mental framework or schema when their level of understanding is initially low.

After a worked example, students should solve problems that are similar to the worked example, only progressing onto the next problem type once they have demonstrated mastery of the previous one. This way, one can avoid asking students to solve problems that overload their working memory capacity.

The explanations of worked examples and practice questions should leverage subgoal labeling by grouping steps into meaningful units. This minimizes the number of chunks of information that students need to store in their working memory, thereby reducing cognitive load. Additionally, subgoal labeling has been shown to help students grasp the structure of the problem, thereby enabling the learning to transfer to novel problems in the same category (Catrambone, 1995).

Explanations should also leverage dual-coding theory by including visualizations and diagrams when possible to help students develop mental images. In addition to helping students make connections that they can use to recall information and consolidate information into chunks, this also helps students avoid cognitive overload by distributing cognitive load more evenly between two subsystems within the working memory system: the phonological loop, which stores verbal information, and the visuo-spatial sketchpad, which stores visual imagery (Baddeley, 1983).

Expertise Reversal Effect

Lastly, note that while it’s important to use scaffolding to minimize cognitive load when students are learning new material, it’s also important to gradually strip away the scaffolding as they become comfortable with that material so that the scaffolding does not become a crutch. This phenomenon is known as the expertise reversal effect: the instructional techniques that promote the most learning in beginners, promote the least learning in experts, and vice versa.

For instance, while initial lessons should be scaffolded by having students solve questions that are similar to worked examples (one worked example at a time), review problems should be mixed up so that it is not obvious which worked example is the best reference. This encourages students to solve review problems without referring to the worked examples – and while they can dig up a similar example for reference if they get really stuck on a review problem, even students who do this must reason about the structure of their problem to match it to helpful reference material.

References

Alloway, T. P., & Alloway, R. G. (2010). Investigating the predictive roles of working memory and IQ in academic attainment. Journal of experimental child psychology, 106(1), 20-29.

Baddeley, A. D. (1983). Working memory. Philosophical Transactions of the Royal Society of London. B, Biological Sciences, 302(1110), 311-324.

Catrambone, R. (1995). Aiding subgoal learning: Effects on transfer. Journal of educational psychology, 87(1), 5.

Swanson, H. L., & Beebe-Frankenberger, M. (2004). The relationship between working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties. Journal of educational psychology, 96(3), 471.

Sweller, J. (2006). The worked example effect and human cognition. Learning and instruction.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.