Chain Rule

by Justin Skycak (@justinskycak) on January 05, 2019

When taking derivatives of compositions of functions, we can ignore the inside of a function as long as we multiply by the derivative of the inside afterwards.

This post is part of the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). Chain Rule. In Justin Math: Calculus. https://justinmath.com/chain-rule/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

The chain rule tells us how to take derivatives of compositions of functions. Informally, it says that we can “forget” about the inside of a function when we take the derivative, as long as we multiply by the derivative of the inside afterwards.

For example, to differentiate $(x^2+1)^{100}$, we can use the power rule, as long as we multiply by the derivative of the inside $(x^2+1)$ afterwards.

$\begin{align*} \left[ (x^2+1)^{100} \right]' &= 100 (x^2+1)^{99} (x^2+1)' \\ &= 100(x^2+1)^{99}(2x) \\ &= 200x(x^2+1)^{99} \end{align*}$

Substitution

More precisely, the chain rule states that we can make a substitution $u$ for an expression of $x$, as long as we multiply by the derivative of the substitution afterwards.

$\begin{align*} \frac{df}{dx} = \frac{df}{du} \frac{du}{dx} \end{align*}$

To differentiate the function $f(x)=(x^2+1)^{100}$, we substituted $u=x^2+1$ to simplify the function to $f(u)=u^{100}$.

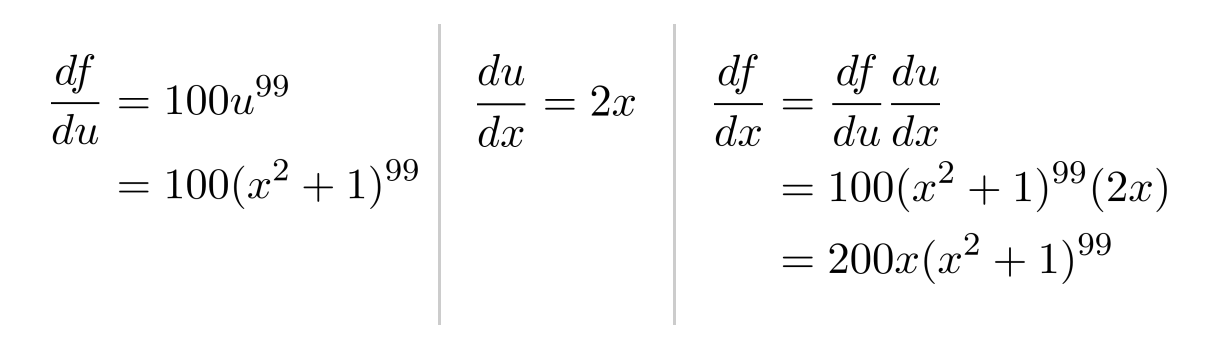
Intuitively, the chain rule says that we can cancel derivatives just like we cancel fractions.

$\begin{align*} \frac{df}{dx} = \frac{df}{du\hspace{-0.5cm}\textbf{---}} \frac{du\hspace{-0.5cm}\textbf{---}}{dx} \end{align*}$

We can extend this to an unlimited number of substitutions, building a “chain” of cancellations.

$\begin{align*} \frac{df}{dx} = \frac{df}{du_1\hspace{-0.75cm}\textbf{------}} \frac{du_1\hspace{-0.75cm}\textbf{------}}{du_2\hspace{-0.75cm}\textbf{------}} \frac{du_2\hspace{-0.75cm}\textbf{------}}{du_3\hspace{-0.75cm}\textbf{------}} \cdots \frac{du_{n-1}\hspace{-1.25cm}\textbf{------}}{du_n\hspace{-0.75cm}\textbf{------}} \frac{du_n\hspace{-0.75cm}\textbf{------}}{dx} \end{align*}$

For example, to differentiate the function $f(x)=(((x^3+1)^4+1)^5+1)^6$ we can proceed one layer at a time.

$\begin{align*} \left[ (((x^3+1)^4+1)^5+1)^6 \right]' &=6(((x^3+1)^4+1)^5+1)^5 \\ &\hspace{.5cm} \cdot \left[ ((x^3+1)^4+1)^5+1 \right]' \\[5pt] &=6(((x^3+1)^4+1)^5+1)^5 \\ &\hspace{.5cm}\cdot 5((x^3+1)^4+1)^4 \\ &\hspace{.5cm}\cdot \left[ (x^3+1)^4+1 \right]' \\[5pt] &=6(((x^3+1)^4+1)^5+1)^5 \\ &\hspace{.5cm}\cdot 5((x^3+1)^4+1)^4 \\ &\hspace{.5cm}\cdot 4(x^3+1)^3 \\ &\hspace{.5cm}\cdot \left[ x^3+1 \right]' \\[5pt] &=6(((x^3+1)^4+1)^5+1)^5 \\ &\hspace{.5cm}\cdot 5((x^3+1)^4+1)^4 \\ &\hspace{.5cm}\cdot 4(x^3+1)^3 \\ &\hspace{.5cm}\cdot 3x^2 \end{align*}$

Exercises

Use the chain rule to find the derivatives of the following functions. (You can view the solution by clicking on the problem.)

$\begin{align*}1) \hspace{.5cm} f(x)=(2x^2+1)^3 \end{align*}$

Solution:
$\begin{align*} f'(x)= 12x(2x^2+1)^2 \end{align*}$

$\begin{align*}2) \hspace{.5cm} f(x)= (x^4-x^2)^8 \end{align*}$

Solution:
$\begin{align*} f'(x)= 8(4x^3-2x)(x^4-x^2)^7 \end{align*}$

$\begin{align*}3) \hspace{.5cm} f(x)=4 \sqrt{ x^2+1 } \end{align*}$

Solution:
$\begin{align*} f'(x)= \frac{x}{\sqrt{x^2+1}} \end{align*}$

$\begin{align*}4) \hspace{.5cm} f(x)=\sqrt{ (2x+1)^2+3 } \end{align*}$

Solution:
$\begin{align*} f'(x)= \frac{4x+2}{ \sqrt{(2x+1)^2+3}} \end{align*}$

$\begin{align*}5) \hspace{.5cm} f(x)= \frac{1}{3x-2} \end{align*}$

Solution:
$\begin{align*} f'(x)= \frac{-3}{(3x-2)^2} \end{align*}$

$\begin{align*}6) \hspace{.5cm} f(x)= \frac{7}{(x^2-3)^2} \end{align*}$

Solution:
$\begin{align*} f'(x)= \frac{-28x}{(x^2-3)^2} \end{align*}$

$\begin{align*}7) \hspace{.5cm} f(x)= \frac{2}{\sqrt{1-x^5} } \end{align*}$

Solution:
$\begin{align*} f'(x)= \frac{-5x^4}{(1-x^5)^\frac{3}{2} } \end{align*}$

$\begin{align*}8)\hspace{.5cm} f(x) = \sqrt{ \sqrt{x} + 1} \end{align*}$

Solution:
$\begin{align*} f'(x)= \frac{1}{ 4 \sqrt{x} \sqrt{ \sqrt{x} + 1 } } \end{align*}$

$\begin{align*}9) \hspace{.5cm} f(x) = \left( \sqrt{x}+1 \right)^5 \end{align*}$

Solution:
$\begin{align*} f'(x)= \frac{ 5 \left( \sqrt{x} + 1 \right)^4 }{2 \sqrt{x} } \end{align*}$

$\begin{align*}10) \hspace{.5cm} f(x) =\left( x^\frac{3}{2} + x^\frac{4}{3} \right)^\frac{5}{4} \end{align*}$

Solution:
$\begin{align*} f'(x) = \frac{5}{4} \left( x^\frac{3}{2} + x^\frac{4}{3} \right)^\frac{1}{4} \left( \frac{3}{2} x^\frac{1}{2} + \frac{4}{3} x^\frac{1}{3} \right) \end{align*}$

This post is part of the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). Chain Rule. In Justin Math: Calculus. https://justinmath.com/chain-rule/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.