Canonical and Reduced Game Trees for Tic-Tac-Toe

by Justin Skycak (@justinskycak) on March 01, 2022

Building data structures that represent all the possible outcomes of a game.

This post is part of the book Introduction to Algorithms and Machine Learning: from Sorting to Strategic Agents. Suggested citation: Skycak, J. (2022). Canonical and Reduced Game Trees for Tic-Tac-Toe. In Introduction to Algorithms and Machine Learning: from Sorting to Strategic Agents. https://justinmath.com/canonical-and-reduced-game-trees-for-tic-tac-toe/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

A game tree is a data structure that represents all the possible outcomes of a game. It is a graph where the nodes correspond to the states of the game, and the edges correspond to actions that cause the game to transition from one state to another. Game trees are commonly used when coding up strategies for autonomous game-playing agents.

Exercise: Tic-Tac-Toe Tree

Create a class TicTacToeTree that constructs a game tree for tic-tac-toe. Each node in the game tree has corresponds to a state of the game. The root node represents an empty board. It has 9 children, one for each move that the first player can make. Each of those 9 children have 8 children (after the first player has moved, there are 8 moves remaining for the second player). And so on.

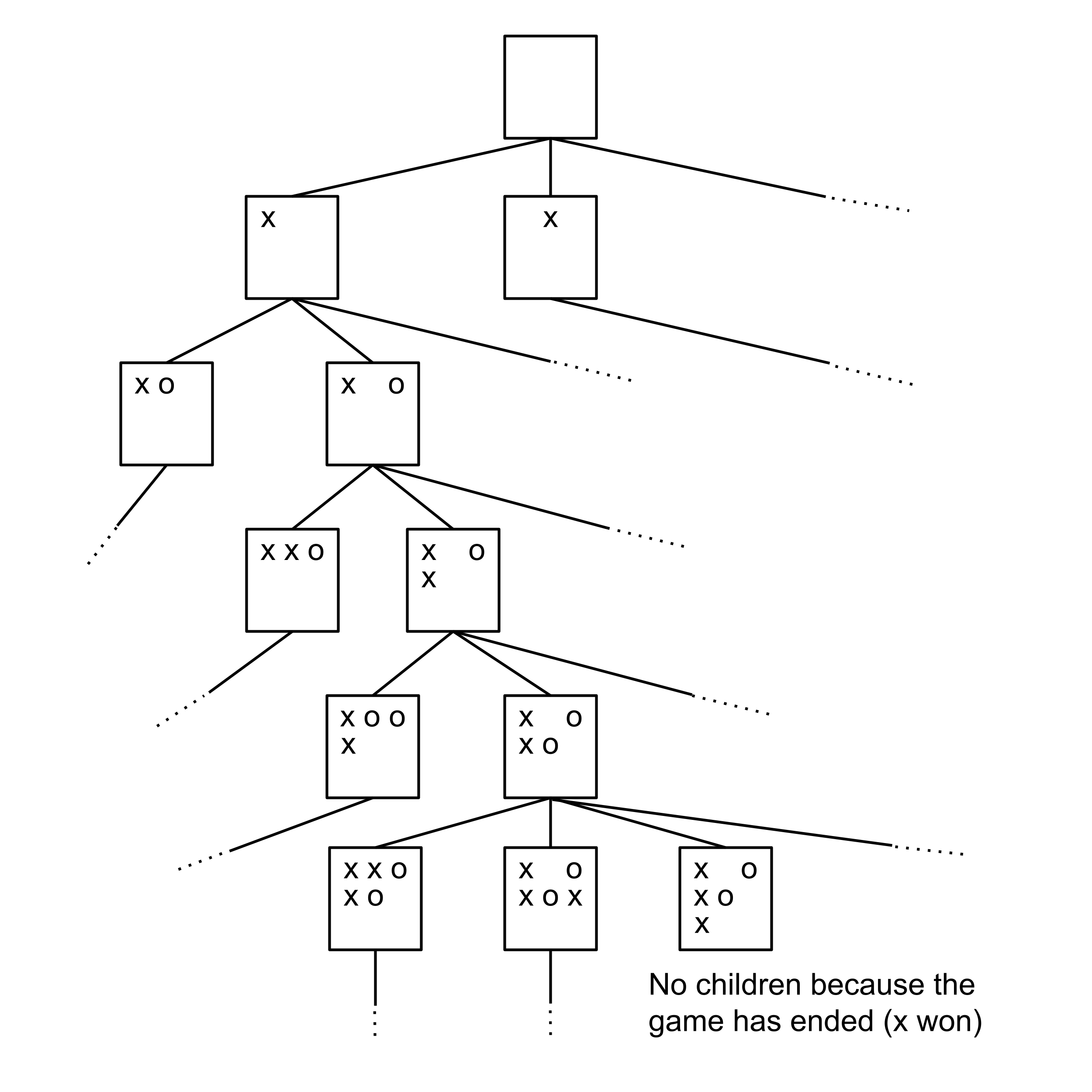
There are $255 \, 168$ unique ways that a game of tic-tac-toe can play out, so you can check your tree by verifying that there are $255 \, 168$ leaf nodes.

Here are some tips regarding the implementation:

Each node should have a state attribute that holds the state of the tic-tac-toe game, a player attribute that says whose turn it is, and a winner attribute that says if someone has won.
Instead of passing edges into the tree at initialization, you'll need to build up your tree algorithmically: start with a tree with a single node, and then repeatedly create child nodes until they reach a terminal state (i.e. a state where the game is finished).
Ultimately this just comes down to a graph traversal (breadth-first or depth-first, doesn't matter which). Whenever a node's game state is not terminal, create a child node for each possible next state.

Exercise: Reduced Tic-Tac-Toe Tree

Once you’ve built your TicTacToeTree and verified that it has the correct number of leaf nodes, the next step is to make it more efficient. Notice that there are many redundancies where separate nodes represent the same state:

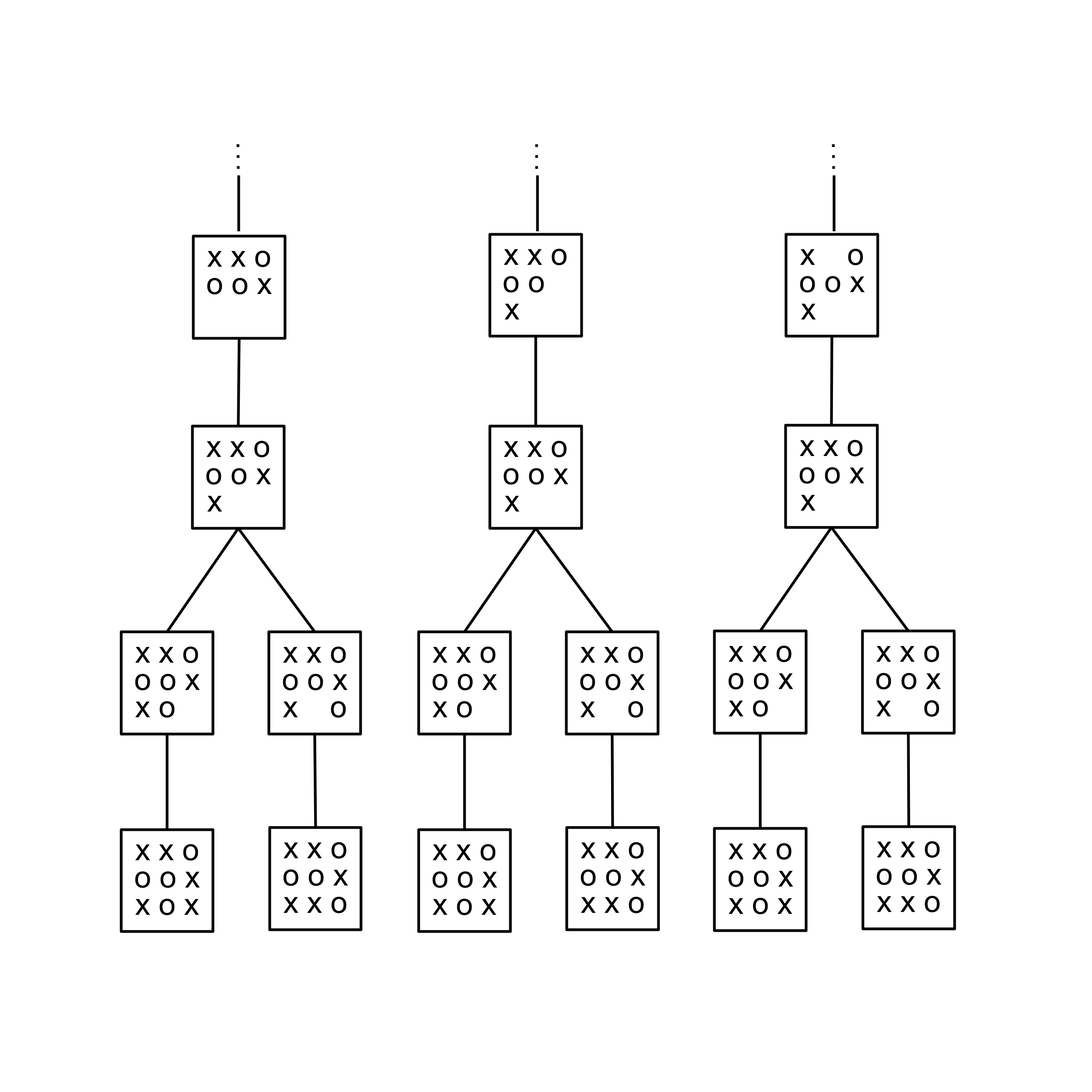
Although redundancies are included in the canonical conception of a game tree, we can greatly speed up the construction and reduce the size of our game tree if we use only one node per game state. To do this, you’ll need to make a slight tweak to your traversal so that whenever a node with the desired state already exists, you connect up that existing node as a child (instead of creating a new node).

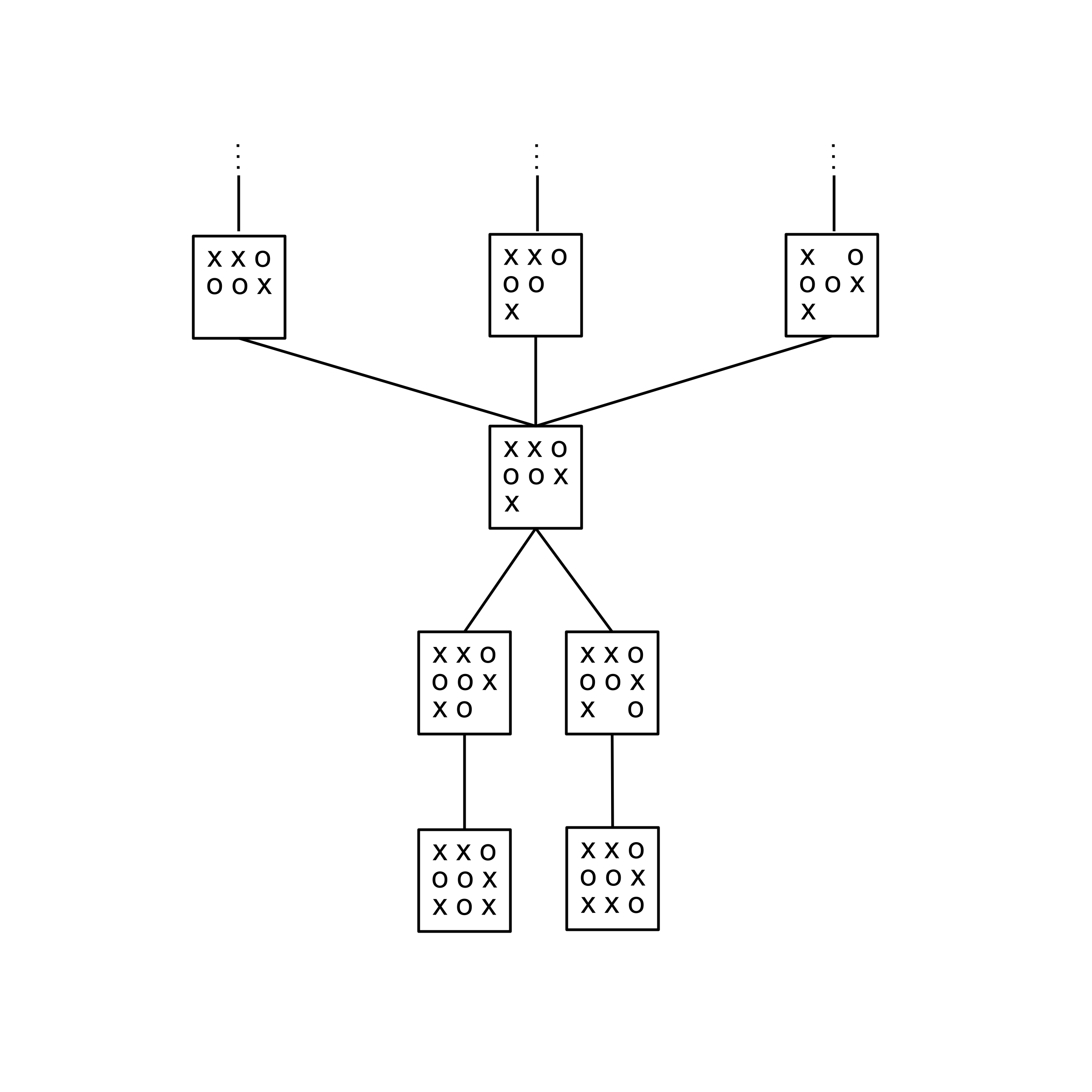
Do not loop over the tree every time to check if a node with the desired child state already exists. That would be really inefficient! Instead, store nodes in a dictionary where the key represents the game state. That way, to check if a node with a particular game state already exists, you just need to look up that state in the dictionary.

There are $5\,478$ distinct possible game states in the game of tic-tac-toe, so you can check your reduced tree by verifying that there are $5\,478$ nodes in total.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.