Applications of Calculus: Understanding Plaque Buildup

by Justin Skycak (@justinskycak) on

Understanding why even slight narrowing of arteries can pose such a big problem to blood flow.

This post is part of the series Connecting Calculus to the Real World.

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

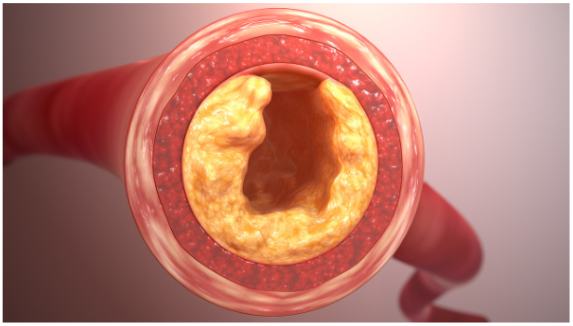
image


Atherosclerosis occurs when fatty deposits, or plaque, builds up to clog arteries. Even seemingly small amounts of plaque can be problematic, because whenever the artery narrows by some percent, the amount of blood that can flow through it decreases by a much greater percent.

Calculus can help us understand how the rate of blood flow through an artery depends on its radius, and why even slight narrowing of arteries can pose such a big problem to blood flow.

Within an artery, blood moves at different speed. The blood near the center of the artery moves the fastest, while the blood near the walls of the artery moves the slowest due to friction against the walls.

When we measure this empirically, we find that if the artery has radius $R,$ then velocity of a blood flow at a radius $r$ from the center is proportional to the difference of squares:

$\begin{align*} v(r) = k(R^2-r^2) \end{align*}$


In order to find how much blood flows through a cross-section of the artery, we can integrate the velocity over the entire area of a cross section:

$\begin{align*} F &= \int v(r) dA \\[5pt] &= \int_0^R k(R^2-r^2) * 2\pi r dr \\[5pt] &= 2 \pi k \int_0^R R^2r - r^3 dr \\[5pt] &= 2\pi k \left[ \frac{R^2r^2}{2} - \frac{r^4}{4} \right]_0^R \\[5pt] &= 2\pi k \left[ \frac{R^4}{2} - \frac{R^4}{4} \right] \\[5pt] &= \pi k R^4 \end{align*}$


This formula is known as Poiseuille’s Law, and it tells us that the flow through an artery is proportional to the fourth power of its radius.

This is why the narrowing of an artery can cause extreme decreases in blood flow. If an artery becomes halfway covered in plaque, then the blood flow becomes even less than half of what it used to be: only $(0.5)^4 = 0.06 = 6\%$ of the blood flow remains.

This post is part of the series Connecting Calculus to the Real World.


Want to get notified about new posts? Join the mailing list and follow on X/Twitter.