Antiderivatives

by Justin Skycak (@justinskycak) on

The antiderivative of a function is a second function whose derivative is the first function.

This post is part of the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). Antiderivatives. In Justin Math: Calculus. https://justinmath.com/antiderivatives/

Want to get notified about new posts? Join the mailing list and follow on X/Twitter.

An antiderivative of a function $f(x)$ is a function $F(x)$ whose derivative is $f(x)$, i.e. $F’(x)=f(x)$.

For example, an antiderivative of $2x$ is $x^2$, because $(x^2)’=2x$. Another antiderivative of $2x$ is $x^2+1$, because $(x^2+1)’ = 2x$. To encapsulate all possibilities, we say that the antiderivative of $2x$ is $x^2+C$ where $C$ is a constant.

The antiderivative of a function $f(x)$ is written symbolically as $\int f(x) \, dx$. For example, to say that the antiderivative of $2x$ is $x^2+C$, we can write $\int 2x \, dx = x^2+C$.

The symbol $\int$ is called an integral, and the differential $dx$ tells us that $x$ is the variable of integration. (The variable of integration may seem unnecessary right now, but it will become more relevant in later chapters when we talk about techniques to solve integrals.)

Power Rule

The power rule for differentiation tells us that $(x^n)’ = nx^{n-1}$. Through a bit of clever intuition, we find a function whose derivative is $x^n$.

$\begin{align*} \left( \frac{1}{n+1} x^{n+1} \right)' = x^n \end{align*}$


Consequently, we have a power rule for integration:

$\begin{align*} \int x^n \, dx = \frac{1}{n+1} x^{n+1} + C \end{align*}$


A few examples are shown below.

$\begin{align*} \int x^2 \, dx = \frac{1}{3}x^3+C \end{align*}$


$\begin{align*} \int \frac{1}{x^5} \, dx &= \int x^{-5} \, dx \\ &= \frac{1}{-4} x^{-4} + C \\ &= -\frac{1}{4x^4} + C \end{align*}$


$\begin{align*} \int \sqrt{x} \, dx &= \int x^{\frac{1}{2}} \, dx \\ &= \frac{1}{3/2} x^{\frac{3}{2}} + C \\ &= \frac{2}{3}x^{\frac{3}{2}} + C \end{align*}$


$\begin{align*} \int 1 \, dx &= \int x^0 \, dx \\ &= \frac{1}{1} x^{1} + C \\ &= x + C \end{align*}$


Integral of the Reciprocal Function

You might notice that if we try to use this power rule to integrate $\frac{1}{x}$, which simplifies to $x^{-1}$, we come up with a nonsense result.

$\begin{align*} \int \frac{1}{x} \, dx &= \int x^{-1} \, dx \\ &= \frac{1}{-1+1}x^0 + C \hspace{.8cm} \mbox{(invalid)} \\ &= \frac{1}{0} + C \hspace{2.65cm} \mbox{(invalid)} \end{align*}$


The case of $n=-1$ is an exception to the power rule, and if we try to perform the power rule anyway, we obtain an invalid result. We will see in a later chapter that, surprisingly, the antiderivative of $\frac{1}{x}$ is $\ln x$.

$\begin{align*} \int \frac{1}{x} \, dx = \ln x + C \end{align*}$


Sum and Constant Multiple Rules

Integrals exhibit some of the same properties as derivatives. For example, the integral of a sum can be computed as the sum of integrals of the integral terms. Also, constants can be moved outside of integrals.

$\begin{align*} &\int 3x^3+x^2-4x+2 \, dx \\ &= \int 3x^3 \, dx + \int x^2 \, dx + \int -4x \, dx + \int 2 \, dx + C \\ &= 3\int x^3 \, dx + \int x^2 \, dx -4\int x \, dx + 2\int 1 \, dx + C \\ &= 3 \left( \frac{1}{4} x^4 \right) + \frac{1}{3}x^3 -4 \left( \frac{1}{2}x^2 \right) + 2(x) + C \\ &= \frac{3}{4} x^4 + \frac{1}{3}x^3 -2 x^2 + 2x + C \end{align*}$


Note that although each individual integral in the sum is associated with a $+C$ constant term, they are redundant, because when we combine all the terms together we still get a constant. Thus, we are able to write a single $+C$ at the very end to account for all constants that arise from the multiple individual integrals.

Integrating Products and Quotients

Unfortunately, there is no simple rule for integrating a product or quotient. We will learn techniques later to make such integrals easier, but for now, the best strategy is to expand out the function as much as possible before trying to take the integral.

For example, to integrate the product $(x+1)(x-1)(x^2+2)$, we can multiply out the product and then integrate each term individually.

$\begin{align*} &\int (x+1)(x-1)(x^2+2) \, dx \\ &= \int (x^2-1)(x^2+2) \, dx \\ &= \int x^4 + x^2 - 2 \, dx \\ &= \frac{1}{5}x^5 + \frac{1}{3}x^3 - 2x + C \end{align*}$


Similarly, to integrate the quotient $\frac{2x^3+x^2-4}{x^2}$, we can split up each term in the numerator and then simplify.

$\begin{align*} & \int \frac{2x^3+x^2-4}{x^2} \, dx \\ &= \int \frac{2x^3}{x^2} + \frac{x^2}{x^2} - \frac{4}{x^2} \, dx \\ &= \int 2x + 1 - 4x^{-2} \, dx \\ &= x^2 + x + 4x^{-1} + C \\ &= x^2 + x + \frac{4}{x} + C \end{align*}$


Integrating Non-Polynomial Functions

Below are some useful rules for finding antiderivatives of non-polynomial functions. (For the sake of readability, the $dx$ and $+C$ have been removed.)

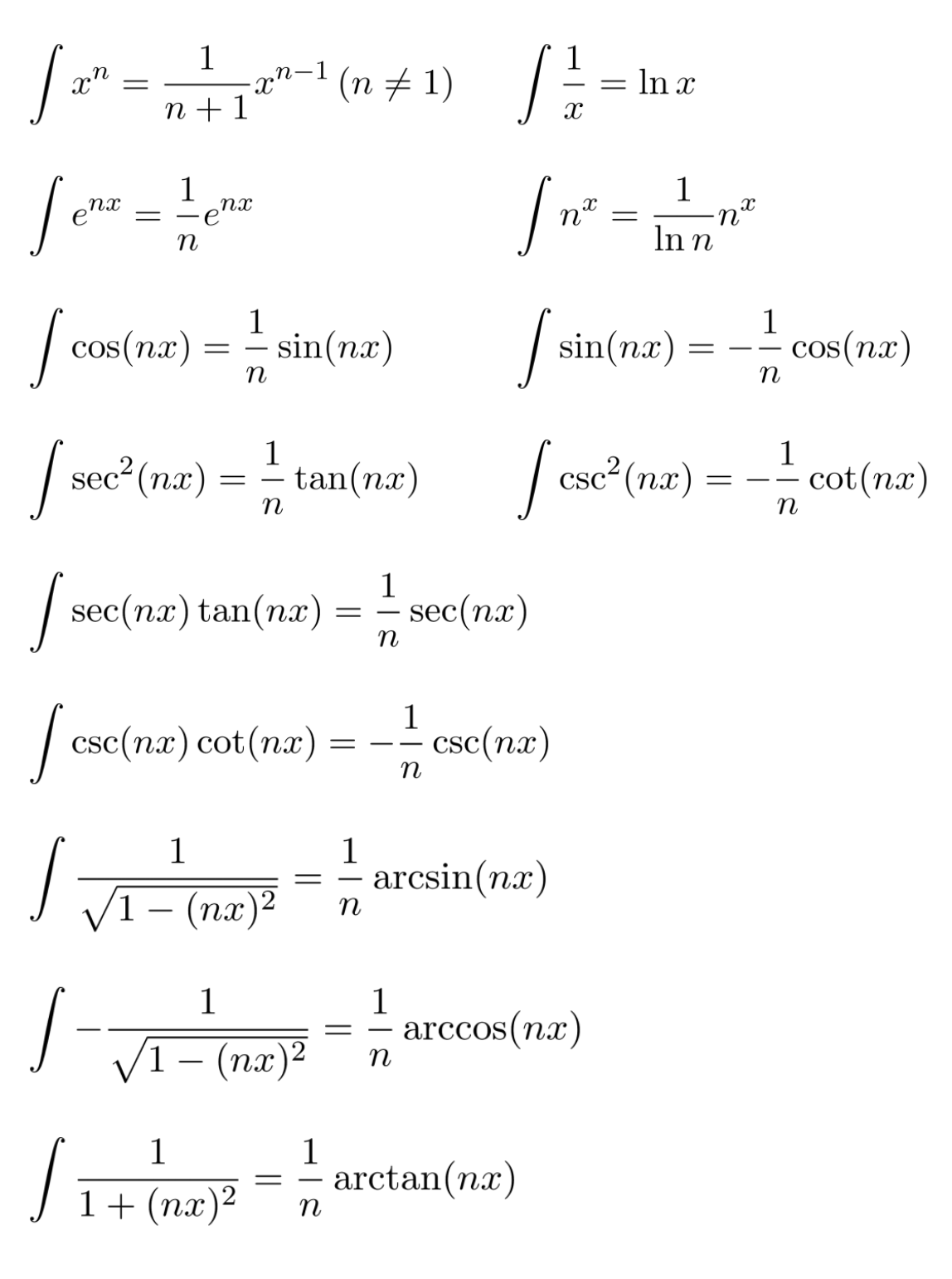
image


Non-polynomial functions can be integrated similarly: we simplify the integral as much as we can, and then find the antiderivative of each term separately. A few examples are shown below.

$\begin{align*} &\int (\sin 3x)\left( 2 + \frac{1}{\cos^2(5x) \sin(3x)} \right) \, dx \\ &= \int 2\sin 3x + \frac{1}{\cos^2 5x } \, dx \\ &= \int 2\sin 3x + \sec^2 5x \, dx \\ &= 2 \int \sin 3x \, dx + \int \sec^2 5x \, dx \\ &= 2 \left( -\frac{1}{3}\cos 3x \right) + \frac{1}{5}\tan 5x + C \\ &= -\frac{2}{3}\cos 3x + \frac{1}{5}\tan 5x + C \end{align*}$


$\begin{align*} &\int \frac{(e^{4x}+3)(e^{4x}-3)}{e^{5x}} + 7 \cdot 2^x + 3^{-x} \, dx \\ &= \int \frac{e^{8x}-9}{e^{5x}} + 7 \cdot 2^x + \left( \frac{1}{3} \right)^{x} \, dx \\ &= \int e^{3x}-9e^{-5x} + 7 \cdot 2^x + \left( \frac{1}{3} \right)^{x} \, dx \\ &= \int e^{3x} \, dx -9 \int e^{-5x} \, dx + 7 \int 2^x \, dx + \int \left( \frac{1}{3} \right)^{x} \, dx \\ &= \frac{1}{3}e^{3x}- 9 \left( \frac{1}{-5}e^{-5x} \right) + 7 \left( \frac{1}{\ln 2} 2^x \right) + \frac{1}{\ln \frac{1}{3} } \left( \frac{1}{3} \right)^{x} + C \\ &= \frac{1}{3}e^{3x} + \frac{9}{5}e^{-5x} + \frac{7}{\ln 2} 2^x + \frac{1}{-\ln 3 } 3^{-x} + C \\ &= \frac{1}{3}e^{3x} + \frac{9}{5}e^{-5x} + \frac{7}{\ln 2} 2^x - \frac{1}{\ln 3 } 3^{-x} + C \end{align*}$


$\begin{align*} &\int \frac{1}{3+2x^2} - \frac{1}{\sqrt{1-4x^2}} \, dx \\ &= \int \frac{1}{3} \left( \frac{1}{1+\frac{2}{3}x^2} \right) - \frac{1}{\sqrt{1-(2x)^2}} \, dx \\ &= \int \frac{1}{3} \left( \frac{1}{1+\left( \sqrt{\frac{2}{3}} x \right) ^2} \right) - \frac{1}{\sqrt{1-(2x)^2}} \, dx \\ &= \frac{1}{3} \int \frac{1}{1+\left( \sqrt{\frac{2}{3}} x \right) ^2} \, dx - \int \frac{1}{\sqrt{1-(2x)^2}} \, dx \\ &= \frac{1}{3} \left( \frac{1}{\sqrt{\frac{2}{3}}} \arctan \sqrt{\frac{2}{3}} x \right) - \frac{1}{2} \arcsin 2x + C \\ &= \frac{1}{\sqrt{6}} \arctan \sqrt{\frac{2}{3}} x - \frac{1}{2} \arcsin 2x + C \end{align*}$


Exercises

Evaluate the following integrals. (You can view the solution by clicking on the problem.)

$\begin{align*}1) \hspace{.5cm} \int x^3-3x^2+\frac{6}{x^4} \, dx \end{align*}$
Solution:
$\begin{align*} \frac{1}{4}x^4 - x^3 - \frac{2}{x^3} + C \end{align*}$


$\begin{align*}2) \hspace{.5cm} \int x \left( 8x^2 - \frac{1}{x} \right) \, dx \end{align*}$
Solution:
$\begin{align*} 2x^4-x+C \end{align*}$


$\begin{align*}3) \hspace{.5cm} \int (x^2+2)^2 \, dx \end{align*}$
Solution:
$\begin{align*} \frac{1}{5}x^5 + \frac{4}{3} x^3 + 4x + C \end{align*}$


$\begin{align*}4) \hspace{.5cm} \int \frac{(x+1)(2x+3)}{3x^2} \, dx \end{align*}$
Solution:
$\begin{align*} \frac{2}{3}x + \frac{5}{3} \ln x - \frac{1}{x} + C \end{align*}$


$\begin{align*}5) \hspace{.5cm} \int 2 \sec^2 3x + \csc \frac{x}{2} \cot \frac{x}{2} \, dx \end{align*}$
Solution:
$\begin{align*} \frac{2}{3} \tan 3x - 2 \csc \frac{x}{2} + C \end{align*}$


$\begin{align*}6) \hspace{.5cm} \int \frac{\sin 3x}{\cos^2 3x} \, dx \end{align*}$
Solution:
$\begin{align*} \frac{1}{3} \sec 3x + C \end{align*}$


$\begin{align*}7) \hspace{.5cm} \int \left( \sin \frac{1}{4} x \right) \left( 3- \frac{4}{\cos^2 4x \sin \frac{1}{4} x } \right) \, dx \end{align*}$
Solution:
$\begin{align*} -12\cos \frac{x}{4} - \frac{4}{5} \tan 5x + C \end{align*}$


$\begin{align*}8) \hspace{.5cm} \int \frac{ \cos (\pi x) - 10}{3 \sin^2 (\pi x) } \, dx \end{align*}$
Solution:
$\begin{align*} -\frac{1}{3\pi} \csc \pi x + \frac{10}{3\pi} \cos \pi x + C \end{align*}$


$\begin{align*}9) \hspace{.5cm} \int e^{4x}-3e^{-3x}+e^{-x} \, dx \end{align*}$
Solution:
$\begin{align*} \frac{1}{4} e^{4x} + e^{-3x} - e^{-x} + C \end{align*}$


$\begin{align*}10) \hspace{.5cm} \int (2e^{3x}-1)(e^{-5x}+2) \, dx \end{align*}$
Solution:
$\begin{align*} -e^{-2x} + \frac{4}{3} e^{3x} + \frac{1}{5} e^{-5x} - 2x + C \end{align*}$


$\begin{align*}11) \hspace{.5cm} \int \frac{ (2e^{4x}-e^{2x})(e^x+1)}{e^{4x}} \, dx \end{align*}$
Solution:
$\begin{align*} 2e^x + 2x + e^{-x} + \frac{1}{2} e^{-2x} + C \end{align*}$


$\begin{align*}12) \hspace{.5cm} \int \frac{ \sqrt{e^{3x} } + 2 }{e^{3x}} \, dx \end{align*}$
Solution:
$\begin{align*} -\frac{2}{3} e^{-\frac{3}{2} x} - \frac{2}{3} e^{-3x} + C \end{align*}$


$\begin{align*}13) \hspace{.5cm} \int \frac{1}{4+4x^2} - \frac{5}{\sqrt{1-x^2}} \, dx \end{align*}$
Solution:
$\begin{align*} \frac{1}{4} \arctan x - 5 \arcsin x + C \end{align*}$


$\begin{align*}14) \hspace{.5cm} \int \frac{2}{1+x^2} + \frac{1}{\sqrt{3-3x^2}} \, dx \end{align*}$
Solution:
$\begin{align*} 2 \arctan x + \frac{1}{\sqrt{3}} \arcsin x + C \end{align*}$


$\begin{align*}15) \hspace{.5cm} \int \frac{1}{1+9x^2} - \frac{3}{\sqrt{1-16x^2}} \, dx \end{align*}$
Solution:
$\begin{align*} \frac{1}{3} \arctan 3x - \frac{3}{4} \arcsin 4x + C \end{align*}$


$\begin{align*}16) \hspace{.5cm} \int \frac{1}{5-10x^2} + \frac{1}{\sqrt{4+9x^2}} \, dx \end{align*}$
Solution:
$\begin{align*} \frac{1}{5 \sqrt{2} } \arctan \sqrt{2} x + \frac{1}{3} \arcsin \frac{3}{2} x + C \end{align*}$


This post is part of the book Justin Math: Calculus. Suggested citation: Skycak, J. (2019). Antiderivatives. In Justin Math: Calculus. https://justinmath.com/antiderivatives/


Want to get notified about new posts? Join the mailing list and follow on X/Twitter.