Absolute value represents the magnitude of a number, i.e. its distance from zero.
This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Absolute Value. In Justin Math: Algebra. https://justinmath.com/absolute-value/
Want to get notified about new posts? Join the mailing list and follow on X/Twitter.
An absolute value function represents the magnitude of a number, i.e. its distance from $0$.
For example, the absolute value of $-3$ is $3$, and the absolute value of $4$ is $4$. We write this as $|-3|=3$, and $|4|=4$.
In effect, absolute value just removes the negative sign from a number, if there is a negative sign to begin with.
Graphs
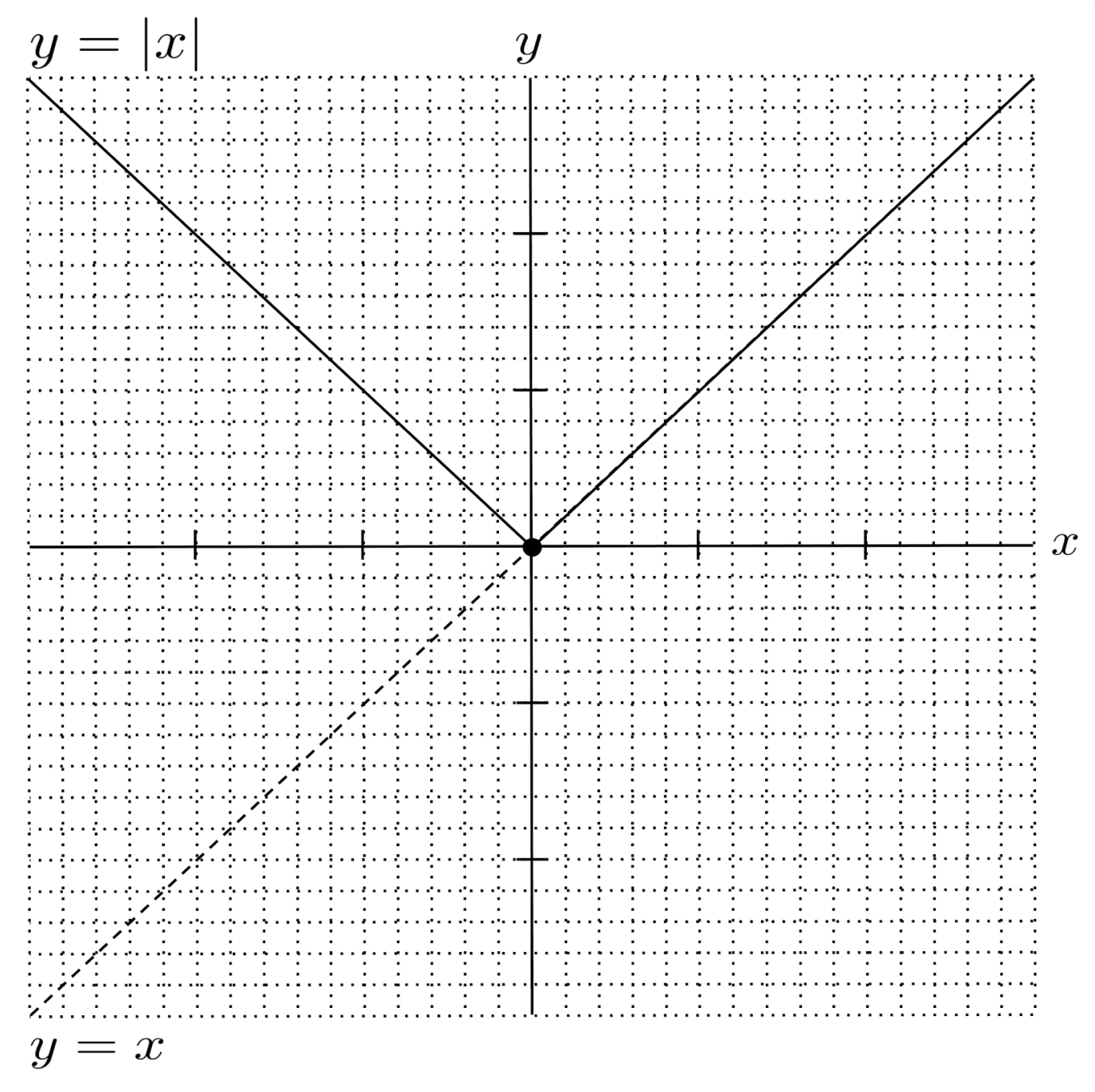
Absolute value graphs are very straightforward – they look similar to the graph of $y=x$, except the the outputs of negative $x$ are turned positive.
Solving Equations by Splitting
Absolute value equations are similar to square root equations, in that we have to consider both positive and negative solutions. For example, the solutions to the equation $|x|=2$ are $x=\pm 2$.
We can usually solve more complicated absolute value equations by isolating the absolute value and then breaking it up into positive and negative equations.
$\begin{align*} \text{Original equation} \hspace{.5cm} &\Bigg| \hspace{.5cm} |x^2-3|-1=0 \\ \text{Isolate the absolute value} \hspace{.5cm} &\Bigg| \hspace{.5cm} |x^2-3|=1 \\ \begin{matrix} \text{Split into positive and} \\ \text{negative equations} \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} \begin{matrix} x^2-3=1 \text{ or} \\ x^2-3=-1 \end{matrix} \\ \text{Solve} \hspace{.5cm} &\Bigg| \hspace{.5cm} x=\pm 2, \pm \sqrt{2} \end{align*}$
Extraneous Solutions
One caveat to solving absolute value equations this way is that if the original equation tells us that the absolute value equals a negative number, we will get the same solutions as if it were a positive number, but none of them will be correct because absolute value can never have a negative output.
$\begin{align*} \text{Original equation} \hspace{.5cm} &\Bigg| \hspace{.5cm} |x^2-3|=-1 \\ \begin{matrix} \text{Split into positive and} \\ \text{negative equations} \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} \begin{matrix} x^2-3=-1 \text{ or} \\ x^2-3=1 \end{matrix} \\ \text{Solve} \hspace{.5cm} &\Bigg| \hspace{.5cm} x=\pm 2, \pm \sqrt{2} \\ \begin{matrix} \text{Check solutions} \\ x=\pm \sqrt{2} \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| \left( \pm \sqrt{2} \right)^2 - 3 \right| = -1 \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| 2-3 \right| = -1 \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| -1 \right| = -1 \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} 1 = -1 \text{ (invalid)} \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \text{ } \\ \begin{matrix} \text{Check solutions} \\ x=\pm 2 \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| \left( \pm 2 \right)^2 - 3 \right| = -1 \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| 4-3 \right| = -1 \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| 1 \right| = -1 \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} 1 = -1 \text{ (invalid)} \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \text{ } \\ \begin{matrix} \text{Remove extraneous} \\ \text{solutions} \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} \text{no solution} \end{align*}$
Whenever an equation tells us that the output of some absolute value is a negative number, the equation will have no solution.
That being said, if an equation tells us that the output of some absolute value is a negative variable expression, the equation might have a solution, because the variable expression itself might be negative at times.
In these cases, it’s usually best to solve the absolute value using the conventional method of splitting up into positive and negative equations, and then check the answers afterward to remove any extraneous solutions.
$\begin{align*} \text{Original equation} \hspace{.5cm} &\Bigg| \hspace{.5cm} |x^2-3|=-2x \\ \begin{matrix} \text{Split into positive and} \\ \text{negative equations} \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} \begin{matrix} x^2-3=-2x \text{ or} \\ x^2-3=2x \end{matrix} \\ \text{Solve} \hspace{.5cm} &\Bigg| \hspace{.5cm} x=\pm 1, \pm 3 \\ \begin{matrix} \text{Check solution} \\ x=1 \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| \left( 1 \right)^2 - 3 \right| = -2(1) \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| 1-3 \right| = -2 \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| -2 \right| = -2 \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} 2 = -2 \text{ (invalid)} \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \text{ } \\ \begin{matrix} \text{Check solution} \\ x=-1 \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| \left( -1 \right)^2 - 3 \right| = -2(-1) \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| 1-3 \right| = 2 \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| -2 \right| = 2 \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} 2 = 2 \text{ (valid)} \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \text{ } \\ \begin{matrix} \text{Check solution} \\ x=3 \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| \left( 3 \right)^2 - 3 \right| = -2(3) \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| 9-3 \right| = -6 \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| 6 \right| = -6 \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} 6 = -6 \text{ (invalid)} \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \text{ } \\ \begin{matrix} \text{Check solution} \\ x=-3 \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| \left( -3 \right)^2 - 3 \right| = -2(-3) \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| 9-3 \right| = 6 \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \left| 6 \right| = 6 \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} 6 = 6 \text{ (valid)} \\ \text{ } \hspace{.5cm} &\Bigg| \hspace{.5cm} \text{ } \\ \begin{matrix} \text{Remove extraneous} \\ \text{solutions} \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} x=-1,-3 \end{align*}$
Case of Multiple Absolute Value Terms
When there are multiple absolute value terms, we need to split the equation into positive and negative equations for each absolute value term, one after the other.
$\begin{align*} \text{Original equation} \hspace{.5cm} &\Bigg| \hspace{.5cm} |x-1|=|x^2-1|+1 \\ \text{ } & \text{ } \\ \begin{matrix} \text{Split into positive and} \\ \text{negative equations} \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} \begin{cases} x-1 = |x^2-1| + 1 \\ x-1 = -|x^2-1|-1 \end{cases} \\ \text{ } & \text{ } \\ \begin{matrix} \text{Isolate remaining} \\ \text{absolute value} \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} \begin{cases} |x^2-1| = x-2 \\ |x^2-1| = -x \end{cases} \\ \text{ } & \text{ } \\ \begin{matrix} \text{Split into positive and} \\ \text{negative equations} \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} \begin{cases} x^2-1=x-2 \\ x^2-1=-x+2 \\ x^2-1=-x \\ x^2-1=x \end{cases} \\ \text{ } & \text{ } \\ \begin{matrix} \text{Split into positive and} \\ \text{negative equations} \end{matrix} \hspace{.5cm} &\Bigg| \hspace{.5cm} \begin{cases} x^2-x+1=0 \\ x^2+x-3=0 \\ x^2+x-1=0 \\ x^2-x-1=0 \end{cases} \\ \text{ } & \text{ } \\ \text{Solve} \hspace{.5cm} &\Bigg| \hspace{.5cm} \begin{cases} \text{no solution} \\ x=\frac{-1\pm \sqrt{13}}{2} \\ x=\frac{-1\pm \sqrt{5}}{2} \\ x=\frac{1\pm \sqrt{5}}{2} \end{cases} \\ \text{ } & \text{ } \\ \text{Combine solutions} \hspace{.5cm} &\Bigg| \hspace{.5cm} x=\frac{-1\pm \sqrt{13}}{2}, \frac{-1\pm \sqrt{5}}{2}, \frac{1\pm \sqrt{5}}{2} \\ \text{Remove extraneous solutions} \hspace{.5cm} &\Bigg| \hspace{.5cm} x=\frac{-1- \sqrt{5}}{2}, \frac{1- \sqrt{5}}{2} \end{align*}$
Exercises
Solve the following absolute value equations. (You can view the solution by clicking on the problem.)
$1) \hspace{.5cm} |x-3|=4$
Solution:
$x = -1,7$
$2) \hspace{.5cm} |3+5x|-7=0$
Solution:
$x = \frac{4}{5}, -2$
$3) \hspace{.5cm} |x-4|+3=0$
Solution:
$\text{no solution}$
$4) \hspace{.5cm} |x^2+1|+2=4$
Solution:
$x = \pm 1$
$5) \hspace{.5cm} |x^2+2x|=8$
Solution:
$x = 2,-4$
$6) \hspace{.5cm} |2x-2|=x$
Solution:
$x = \frac{2}{3},2$
$7) \hspace{.5cm} |2x^2+1|=x+1$
Solution:
$x = 0,\frac{1}{2}$
$8) \hspace{.5cm} |3-4x^2|+x=2$
Solution:
$x = 1,-\frac{5}{4}, \frac{1\pm \sqrt{17}}{8}$
$9) \hspace{.5cm} |x+1|=|x|$
Solution:
$x = -\frac{1}{2}$
$10) \hspace{.5cm} |2x-1|=1-|x|$
Solution:
$x = 0,\frac{2}{3}$
$11) \hspace{.5cm} |x^2-4|=|x|-2$
Solution:
$x = \pm 2$
$12) \hspace{.5cm} |x^2-1|=|2x|-1$
Solution:
$x = \pm 2, 1-\sqrt{3}, -1+\sqrt{3}$
$13) \hspace{.5cm} |x|+|x+1|=|x-1|$
Solution:
$x = -2,0$
$14) \hspace{.5cm} |x|+|2x^2|=|x+1|$
Solution:
$x = \sqrt{ \frac{1}{2} }, \frac{1-\sqrt{3}}{2}$
This post is part of the book Justin Math: Algebra. Suggested citation: Skycak, J. (2018). Absolute Value. In Justin Math: Algebra. https://justinmath.com/absolute-value/
Want to get notified about new posts? Join the mailing list and follow on X/Twitter.
